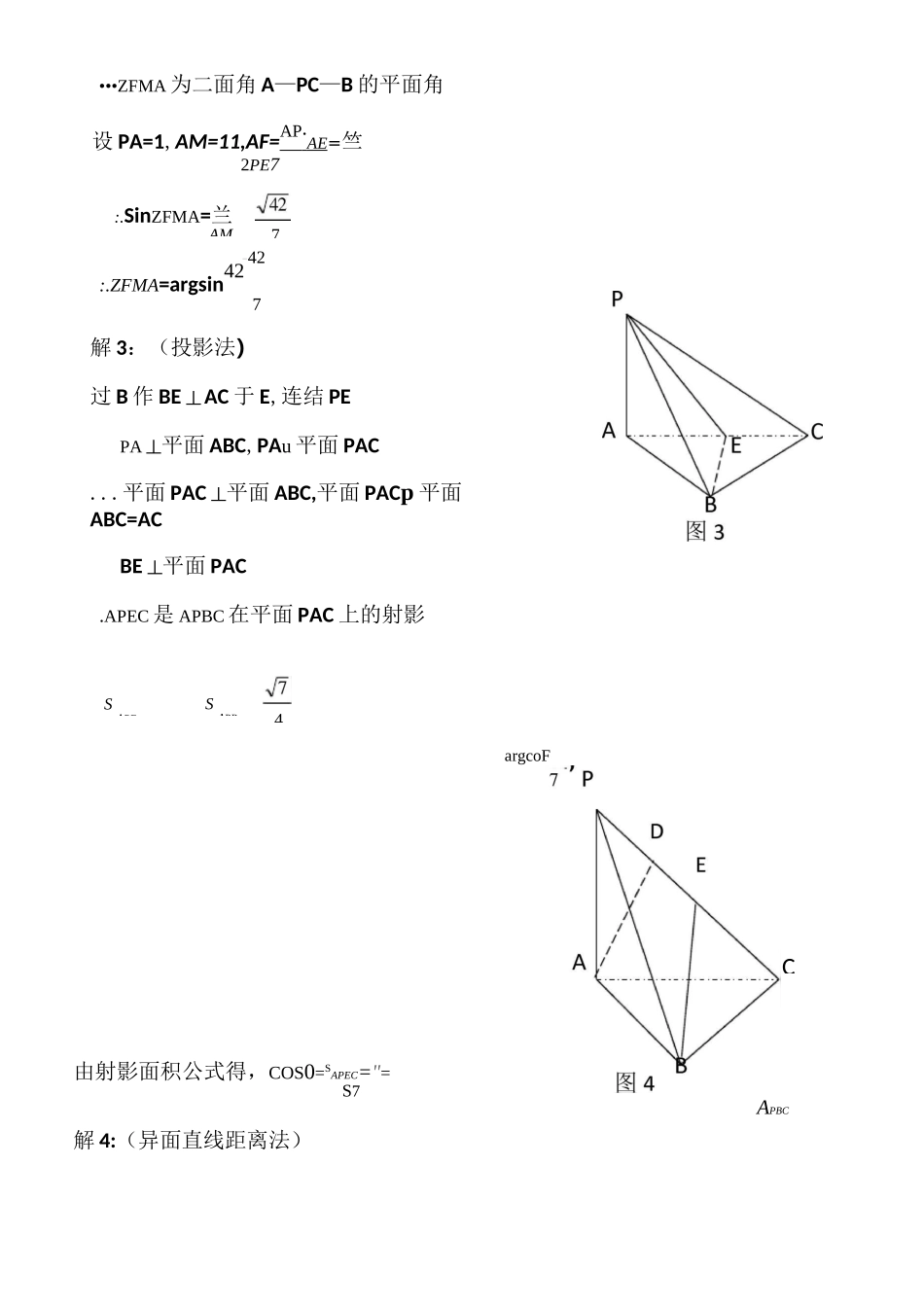
二面角的作与求求角是每年高考必考内容之一,可以做为选择题,也可作为填空题,时常作为解答题形式出现,重点把握好二面角,它一般出现在解答题中.下面就对求二面角的方法总结如下:1、定义法:在棱上任取一点,过这点在两个面内分别引棱的垂线,这两条射线所成的角就是二面角的平面角。2、三垂线定理及逆定理法:自二面角的一个面上的一点向另一个面引垂线,再由垂足向棱作垂线得到棱上的点.斜足与面上一点连线,和斜足与垂足连线所夹的角即为二面角的平面角。3、作棱的垂面法:自空间一点作与棱垂直的平面,截二面角的两条射线所成的角就是二面角的平面角.4、投影法:利用 s=scose 这个公式对于斜面三角形,任意多边形都成立,是求投影面被投影面二面角的好方法。尤其对无棱问题5 异面直线距离法:EF2=m2+n2+d2—2mncose例 1:若 p 是 AABC 所在平面外一点,而 APBC 和 AABC 都是边长为 2 的正三角形,PA=十:6,求二面角 P—BC-A 的大小.分析:由于这两个三角形是全等的三角形故采用定义法解:取 BC 的中点 E,连接 AE、PEAC=AB,PB=PCAE 丄BC,PE 丄BC•••ZPEA 为二面角 P—BC—A 的平面角在 APAE 中 AE=PE=「3,PA=订 6BZPEA=90o二面角 P—BC-A 的平面角为 9Oo.例 2:已知 AABC 是正三角形,PA 丄平面 ABC 且 PA=AB=a,求二面角 A—PC-B 的大小.[思维]二面角的大小是由二面角的平面角来度量的,本题可利用三垂线定理(逆)来作平面角,还可以用射影面积公式或异面直线上两点间距离公式求二面角的平面角。解 1:(三垂线定理法)取 AC 的中点 E,连接 BE,过 E 做 EF 丄PC,连接 BFPA 丄平面 ABC,PAu 平面 PAC...平面 PAC 丄平面 ABC,平面 PACp 平面 ABC=ACBE 丄平面 PAC由三垂线定理知 BF 丄PC.ZBFE 为二面角 A-PC—B 的平面角设 PA=1,E 为 AC 的中点,BE=2^,EF^224BE_tanZBFE=——6EF:.ZBFE=arctan\6解 2:(三垂线定理法)取 BC 的中点 E,连接 AE,AB=AC,PB=PCAE 丄BC,PE 丄BCBC 丄平面 PAE,BCu平面 PBC平面 PAE 丄平面 PBC,由三垂线定理知 AM 丄PCPE 过 A 做 AF 丄PE,FM 丄PC,连接F:.SinZFMA=兰AM-42:.ZFMA=argsin427解 3:(投影法)过 B 作 BE 丄AC 于 E,连结 PEPA 丄平面 ABC,PAu 平面 PAC...平面 PAC 丄平面 ABC,平面 PACp 平面ABC=ACBE 丄平面 PAC.APEC 是 APBC 在平面 PAC 上的射影SAPESAPBargcoF•••ZFMA 为二...