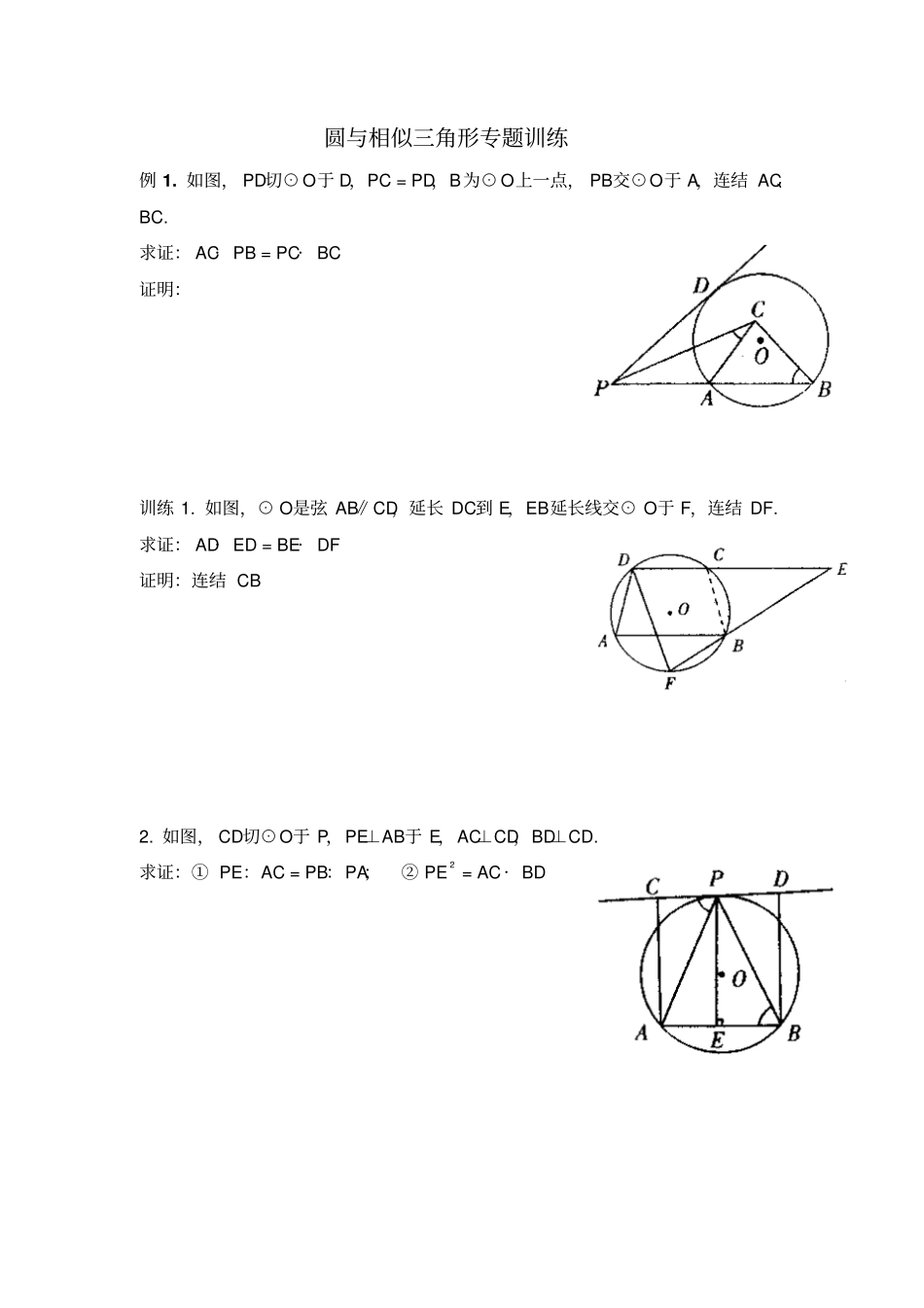
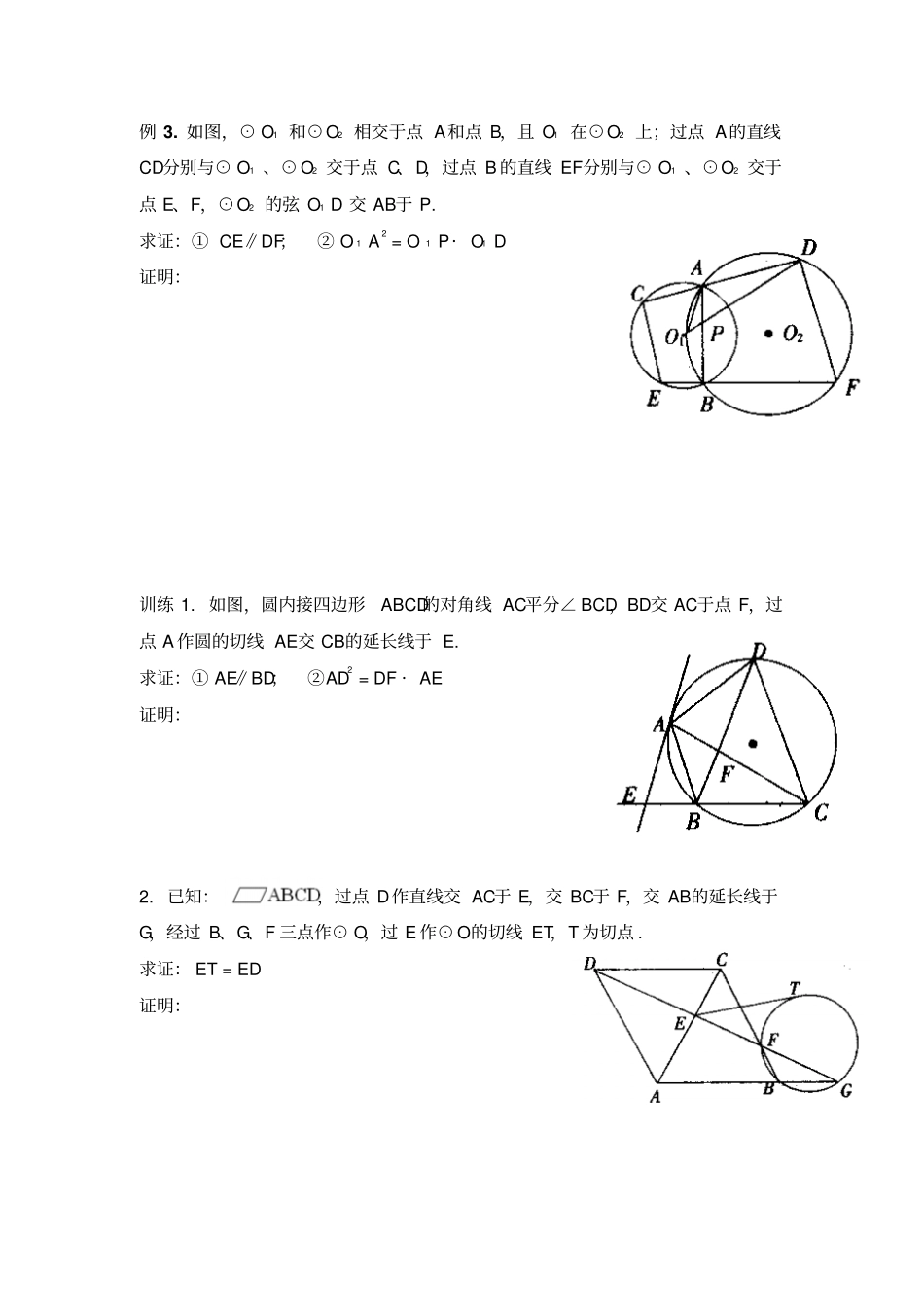
圆与相似三角形专题训练例 1. 如图, PD切⊙ O于 D,PC = PD,B为⊙ O上一点, PB交⊙O于 A,连结 AC、BC. 求证: AC· PB = PC· BC 证明:训练 1. 如图,⊙ O是弦 AB∥CD,延长 DC到 E,EB延长线交⊙ O于 F,连结 DF. 求证: AD· ED = BE· DF 证明:连结 CB 2. 如图, CD切⊙O于 P,PE⊥AB于 E,AC⊥CD,BD⊥CD. 求证:① PE:AC = PB:PA;② PE 2 = AC· BD 例 2. 如图,△ ABC内接于⊙ O,⊙ O的直径 BD交 AC于 E,AF⊥BD于 F,延长 AF交 BC于 G. 求证: AB 2 = BG· BC 证明:连结 AD 训练 1. 如图, AB是⊙ O的直径,弦 CD垂直 AB于 M,P是 CD延长线上一点, PE切⊙ O于 E,BE交 CD于 F. 求证: PF 2 = PD · PC 证明:连结 AE2. 如图,△ ABC中,AB = AC,O是 BC上一点,以 O为圆心, OB长为半径的圆与AC相切于点 A,过点 C作 CD⊥BA,垂足为 D. 求证:①∠DAC = 2∠B;② CA 2 = CD· CO 例 3. 如图,⊙ O 1 和⊙O 2 相交于点 A和点 B,且 O 1 在⊙O 2 上;过点 A的直线CD分别与⊙ O1 、⊙ O2 交于点 C、D,过点 B 的直线 EF分别与⊙ O1 、⊙O2 交于点 E、F,⊙O 2 的弦 O 1 D 交 AB于 P. 求证:① CE∥DF;② O 1 A2 = O 1 P· O 1 D 证明:训练 1. 如图,圆内接四边形ABCD的对角线 AC平分∠ BCD,BD交 AC于点 F,过点 A 作圆的切线 AE交 CB的延长线于 E. 求证:① AE∥BD;②AD 2 = DF · AE 证明:2. 已知:,过点 D作直线交 AC于 E,交 BC于 F,交 AB的延长线于G,经过 B、G、F 三点作⊙ O,过 E 作⊙ O的切线 ET,T 为切点 . 求证: ET = ED 证明:DCBAOEF3. 如图, AB、AC分别切⊙ O于 M、N,且 BE = EF = FC. 求证: AB = AC 证明:4. 如图, A 是⊙ O上一点,割线 PC交⊙ O于 B、C 两点, D是 PC上的一点,且PD是 PB和 PC的比例中项, PD = PA,连结 AD,并延长交⊙ O于点 E. 求证: BE = CE 证明:5. 如图,△ ABC中,AC = BC,以 BC为直径的圆与 AB、AC分别交于 P、Q,过 P的切线交 AC于 M. 求证:① PM⊥AC;②AM = MQ 6.如图,⊿ ABC 内接于⊙ O,且 BC 是⊙ O 的直径, AD⊥BC 于 D,F 是弧 BC 中点,且 AF交 BC 于 E,AB=6,AC= 8,求 CD, DE,及 EF 的长.