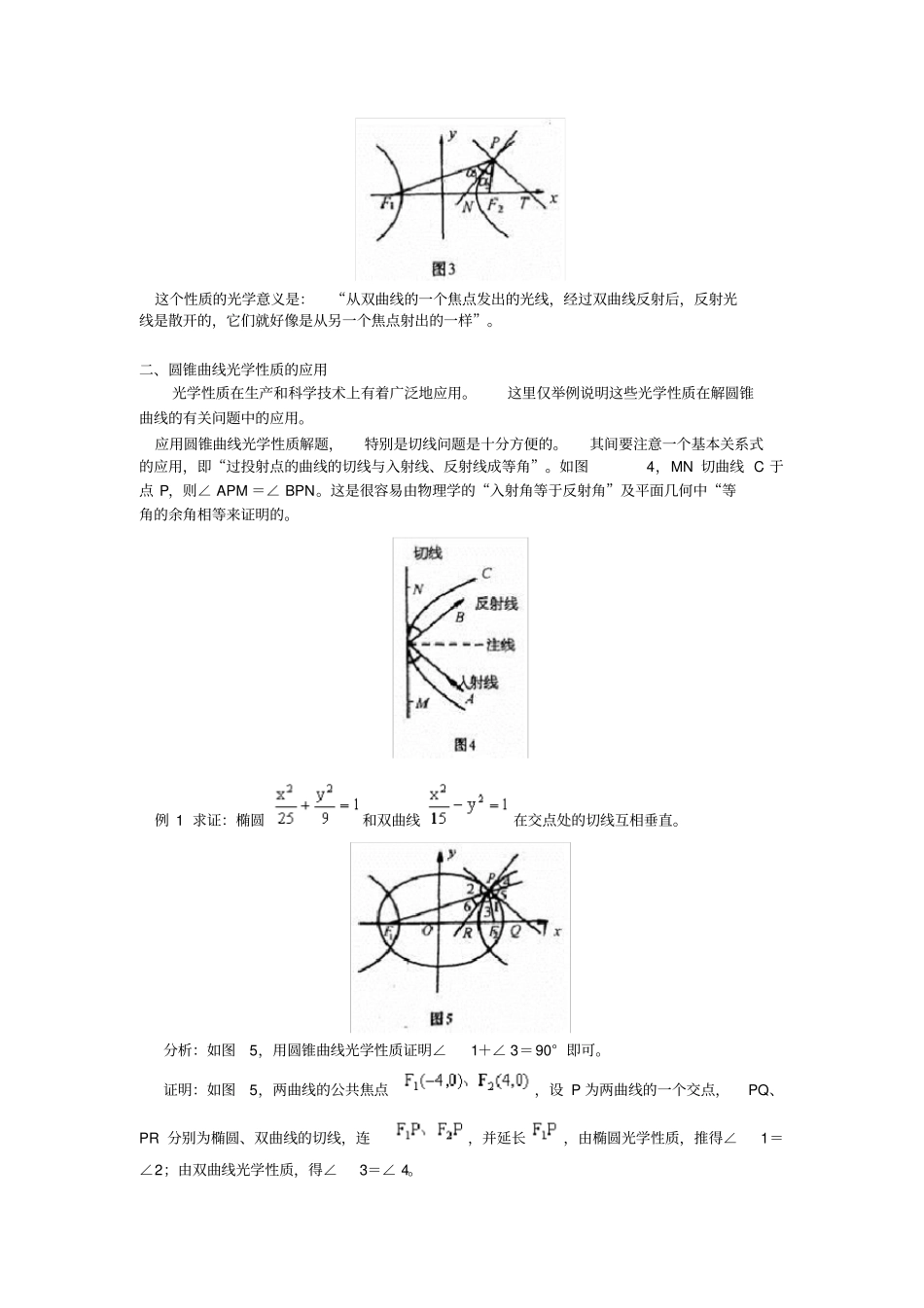
圆锥曲线的光学性质及其应用尹建堂一、圆锥曲线的光学性质圆锥曲线的光学性质源于它的切线和法线的性质,因而为正确理解与掌握其光学性质,就要掌握其切线、法线方程的求法及性质。设 P()为圆锥曲线(A 、B、C 不同时为零)上一定点,则在该点处的切线方程为:。(该方程与已知曲线方程本身相比,得到的规律就是通常所说的“替换法则”,可直接用此法则写出切线方程)。该方程的推导,原则上用“△法”求出在点P 处的切线斜率,进而用点斜 式 写 出 切 线 方 程, 则 在 点P处 的 法 线 方 程 为。1、抛物线的切线、法线性质经过抛物线上一点作一条直线平行于抛物线的轴,那么经过这一点的法线平分这条直线和这一点的焦半径的夹角。如图1 中。事实上,设为抛物线上一点,则切线MT 的方程可由替换法则,得,即,斜率为,于是得在点M 处的法线方程为令,得法线与x 轴的交点 N 的坐标为,所以又焦半径所以,从而得即当点 M 与顶点 O 重合时,法线为x 轴,结论仍成立。所以过 M 的法线平分这条直线和这一点的焦半径的夹角。也可以利用点M 处的切线方程求出,则,又故,从而得也可以利用到角公式来证明抛物线的这个性质的光学意义是:“从焦点发出的光线,经过抛物线上的一点反射后,反射光线平行于抛物线的轴”。2、椭圆的切线、法线性质经过椭圆上一点的法线,平分这一点的两条焦点半径的夹角。如图2 中证明也不难,分别求出,然后用到角公式即可获证。椭圆的这个性质的光学意义是:“从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线交于椭圆的另一个焦点上”。3、双曲线的切线、法线性质经过双曲线上一点的切线,平分这一点的两条焦点半径的夹角,如图3 中。仍可利用到角公式获证。这个性质的光学意义是:“从双曲线的一个焦点发出的光线,经过双曲线反射后,反射光线是散开的,它们就好像是从另一个焦点射出的一样”。二、圆锥曲线光学性质的应用光学性质在生产和科学技术上有着广泛地应用。这里仅举例说明这些光学性质在解圆锥曲线的有关问题中的应用。应用圆锥曲线光学性质解题,特别是切线问题是十分方便的。其间要注意一个基本关系式的应用,即“过投射点的曲线的切线与入射线、反射线成等角”。如图4,MN 切曲线 C 于点 P,则∠ APM =∠ BPN。这是很容易由物理学的“入射角等于反射角”及平面几何中“等角的余角相等来证明的。例 1 求证:椭圆和双曲线在交点处的切线互相垂直。分析:...