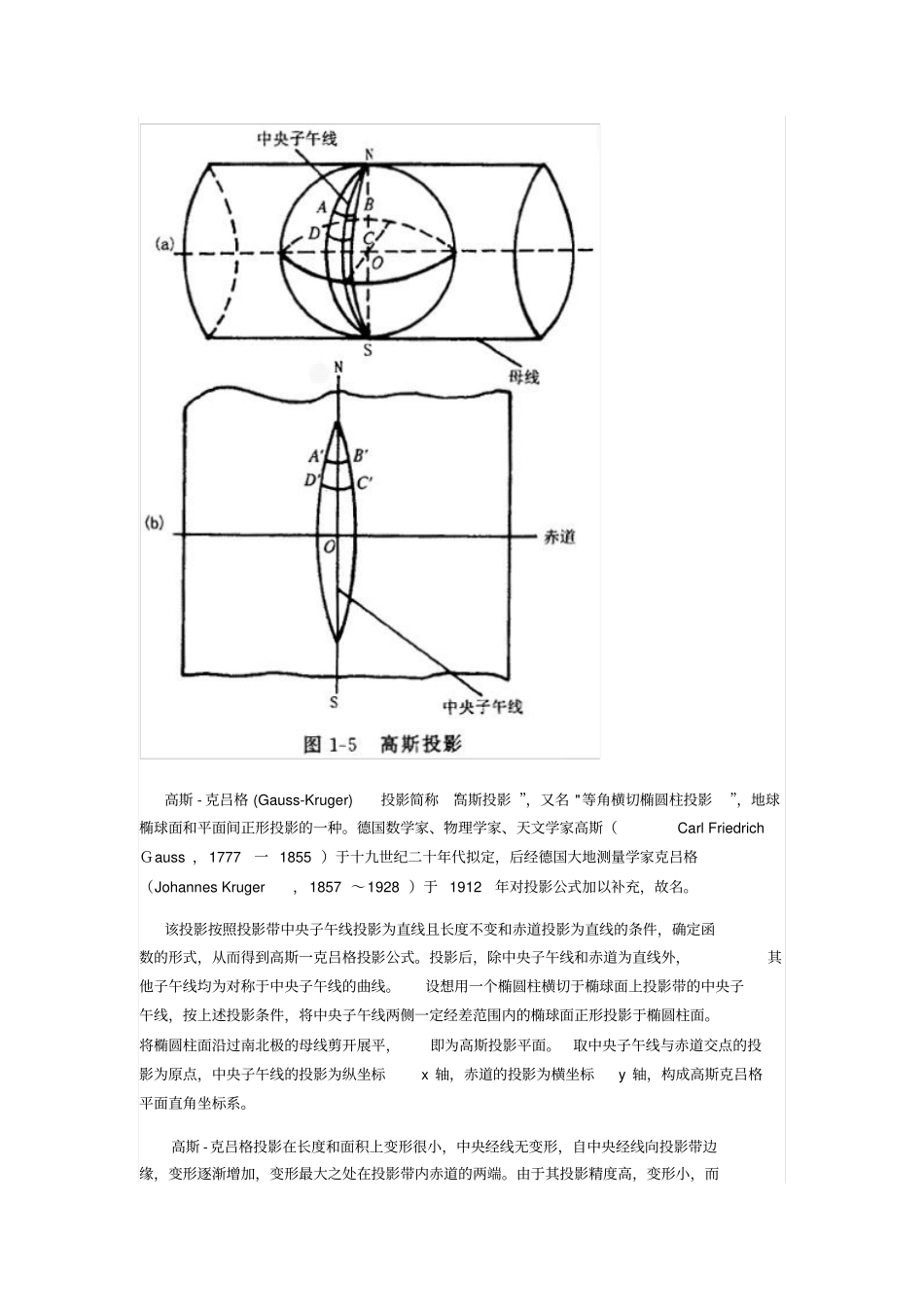
墨卡托投影、高斯 - 克吕格投影、 UTM投影及我国分带方法一、墨卡托投影、高斯-克吕格投影、 UTM投影1 . 墨卡托 (Mercator)投影墨卡托 (Mercator)投影,是一种 "等角正切圆柱投影”,荷兰地图学家墨卡托 (Gerhardus Mercator 1512-1594 )在 1569年拟定,假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触, 然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开, 这就是一幅选定标准纬线上的“墨卡托投影 ”绘制出的地图。 墨卡托投影没有角度变形, 由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。“海底地形图编绘规范”(GB/T 17834-1999,海军航保部起草)中规定 1 :25 万及更小比例尺的海图采用墨卡托投影,其中基本比例尺海底地形图(1 :5 万,1 :25 万,1 :100 万)采用统一基准纬线30 ° ,非基本比例尺图以制图区域中纬为基准纬线。基准纬线取至整度或整分。墨卡托投影坐标系取零子午线或自定义原点经线(L0) 与赤道交点的投影为原点,零子午线或自定义原点经线的投影为纵坐标X 轴,赤道的投影为横坐标Y 轴,构成墨卡托平面直角坐标系。2 . 高斯 - 克吕格 (Gauss-Kruger)投影和 UTM (Universal Transverse Mercator)投影(1 )高斯 -克吕格投影性质高斯 - 克吕格 (Gauss-Kruger)投影简称 “高斯投影 ”,又名 "等角横切椭圆柱投影”,地球椭球面和平面间正形投影的一种。德国数学家、物理学家、天文学家高斯(Carl FriedrichGauss ,1777一 1855 )于十九世纪二十年代拟定,后经德国大地测量学家克吕格(Johannes Kruger,1857 ~1928 )于 1912年对投影公式加以补充,故名。该投影按照投影带中央子午线投影为直线且长度不变和赤道投影为直线的条件,确定函数的形式,从而得到高斯一克吕格投影公式。投影后,除中央子午线和赤道为直线外,其他子午...