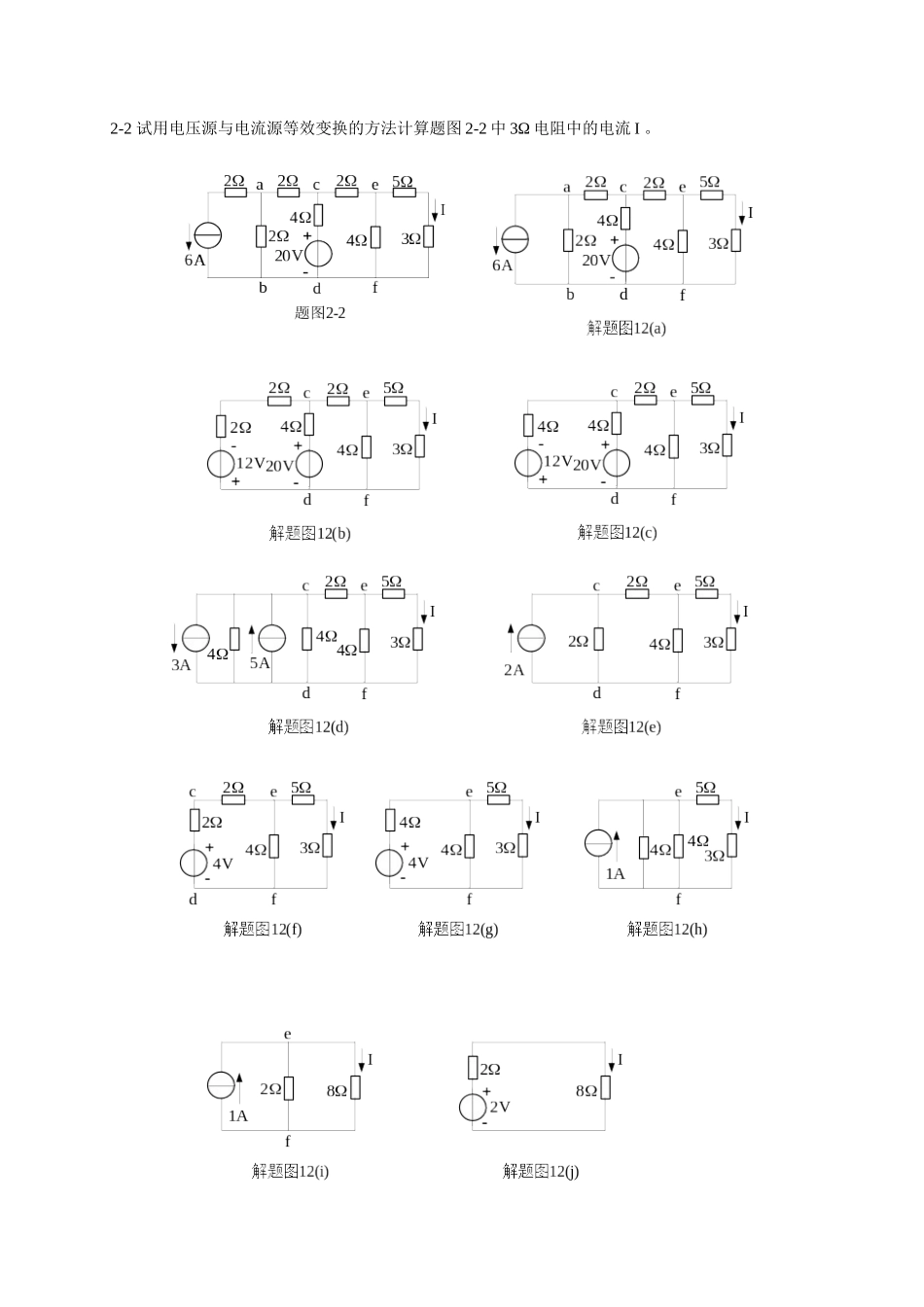
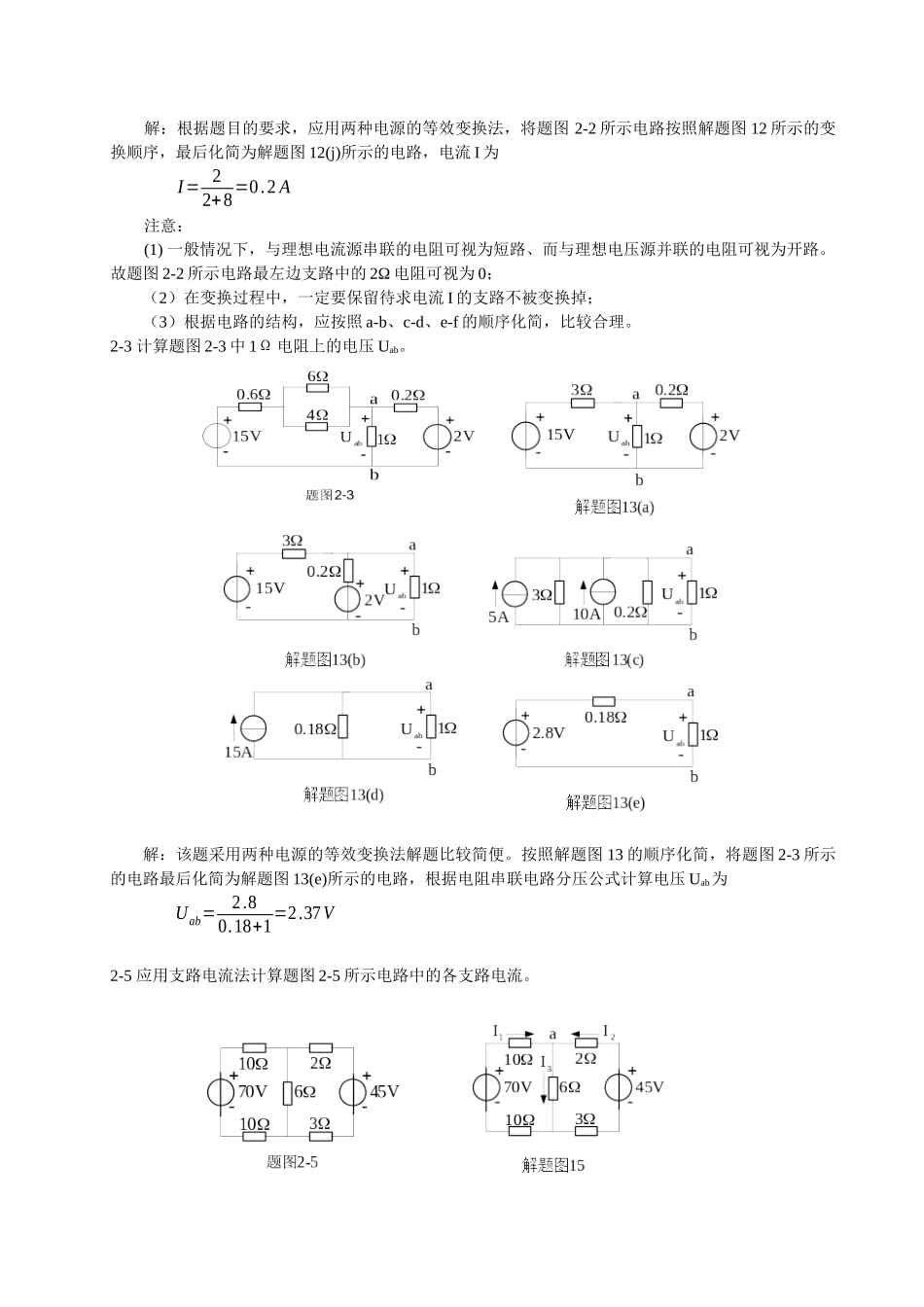
2-2 试用电压源与电流源等效变换的方法计算题图 2-2 中 3Ω 电阻中的电流 I 。解:根据题目的要求,应用两种电源的等效变换法,将题图 2-2 所示电路按照解题图 12 所示的变换顺序,最后化简为解题图 12(j)所示的电路,电流 I 为 I= 22+8=0.2 A注意:(1) 一般情况下,与理想电流源串联的电阻可视为短路、而与理想电压源并联的电阻可视为开路。故题图 2-2 所示电路最左边支路中的 2Ω 电阻可视为 0;(2)在变换过程中,一定要保留待求电流 I 的支路不被变换掉;(3)根据电路的结构,应按照 a-b、c-d、e-f 的顺序化简,比较合理。2-3 计算题图 2-3 中 1Ω 电阻上的电压 Uab。 解:该题采用两种电源的等效变换法解题比较简便。按照解题图 13 的顺序化简,将题图 2-3 所示的电路最后化简为解题图 13(e)所示的电路,根据电阻串联电路分压公式计算电压 Uab为 Uab=2.80.18+1=2.37V2-5 应用支路电流法计算题图 2-5 所示电路中的各支路电流。解:首先对于题图 2-5 所示电路的三条支路电流分别确定参考方向,如解题图 15 所示。然后应用基尔霍夫电流定律和基尔霍夫电压定律定律列出下列三个方程:{I1+I2−I3=0¿{70=10I1+6I3+10I1=20I1+6I3¿¿¿¿解之,得 I 1=2 AI 2=5 AI 3=3 A2-6 应用支路电流法计算题图 2-6 所示电路中的各支路电流。解:如题图 2-6 所示,电路中的四条支路均为并联,其中一条支路电流为已知,根据支路电流法可知,只需列出三个独立方程即可求解。为看图方便,将电路中 4Ω 电阻支路改画到解题图 16 所示的地方,应用基尔霍夫电流定律对结点 a 列出一个电流方程,再应用基尔霍夫电压定律对电路左边回路和中间回路列出两个电压方程,即 {I1−I+I2+10=0¿{120=0.8I1+4I¿¿¿¿解之,得 I 1=9.38 AI 2=8.75 AI=28.13 A2-8 电路如题图 2-8 所示,试用结点电压法计算图中电阻 RL两端电压 U,并计算理想电流源的功率。 解:由于计算负载电阻 RL的电压 U,与理想电流源串联的 4Ω 电阻和与理想电压源并联的 8Ω 电阻的存在与否无关,因此,这两个电阻的作用可被忽略,如解题图 17 所示,那么 U=4+16414 + 14 + 18=12.8V然而,在计算理想电流源的功率时,理想电流源两端的电压值是由与之并联的外电路所确定,因此,与理想电流源串联的 4Ω 电阻的作用就不能被忽略。此时,必须根据题图 2-8 所示电路解题才正确,理想电流源两端的电压应用电...