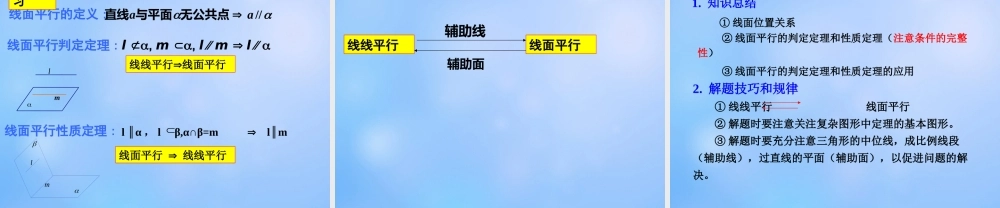
9.3 直线和平面平行与平面和平面平行一 . 直线和平面平行异面直线的所成角范围 :]2,0( 异面直线的本质 : 不相交 , 不平行异面直线的判定定理 :BA 复 习为异面直线。和直线lABlBlBA,,,异面直线的所成角求法 : 一作,二证,三求解二 . 直线和平面的位置关系① 表示为: a β② 表示为: a∩β=A a β③ 表示为: a β∥(2) 一条直线和一个平面只有一个公共点,叫做直线与平面相交。定义:(3) 直线和平面没有公共点,叫做直线与平面平行。(1) 一条直线和一个平面有两个公共点,叫做直线在平面内。(2) 、 (3) 合称“直线不在平面内”。注意:如下画图不规范不表示为: a∩β不表示为: a β∥三 . 线面平行的判定定理 如果不在一个平面内一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行 。l α , m α,l m∥l α∥已知 :求证:证明: l m∥ ∴ l 和 m 确定一平面,设平面 β , 则 α∩β=m如果 l 和平面 α 不平行,则 l 和 α 有公共点设 l ∩α=P ,则点 Pm∈于是 l 和 m 相交,这和 l m∥矛盾 ∴ l α∥线线平行线面平行判定定理的本质:判定定理的用法: l , m , l m l 三个条件中,缺少其中任一个,都不成立四 . 线面平行的性质定理定理 如果一条直线和一个平面平行,经过这条直线的平面 和这个平面相交,那么这条直线就和交线平行。 已知 :l α∥ , l β,α∩β=m求证: l m∥证明: l α∥∴l 和 α 没有公共点, m 在 α内∴l 和 m 也没有公共点∴l 和 m 都在平面 β 内,又没有公共点 ∴ l m∥问题:如果一条直线和一个平面平行,该直线是否与该平面 内所有直线都平行?性质定理的本质: 线面平行 线线平行性质定理的用法: l α∥ , l β,α∩β=ml m∥ 三个条件中,缺少其中任一个,都不成立五 . 例题:例 1. 已知:空间四边形 ABCD 中, E 、 F 分别是 AB 、 AD的中点.求证: EF∥平面 BCD .证明:连结 BD ,在△ ABD 中 E 、 F 分别是 AB 、 AD 的中点∴ EF∥BD其中 BD 是平面 ABD 与平面 BCD 的交线又 EF 平面BCD∴ EF∥ 平面 BCD例 2. 求证:如果过平面内的一点的直线平行于与此平面平行的一条直线,那么这条直线在此平面内。mmPl练...