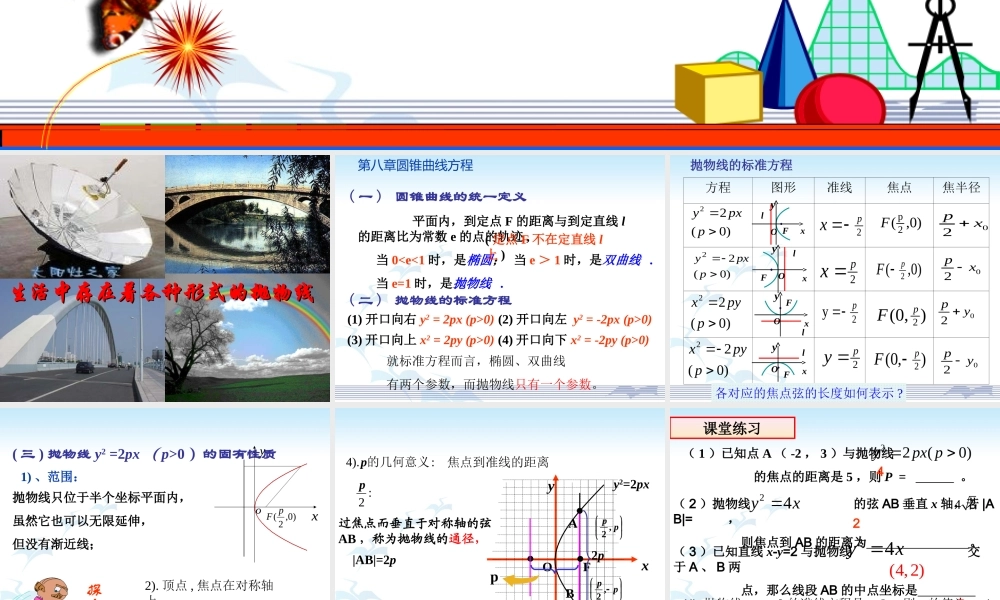
抛物线生活中存在着各种形式的抛物线生活中存在着各种形式的抛物线( 一 ) 圆锥曲线的统一定义 平面内,到定点 F 的距离与到定直线 l的距离比为常数 e 的点的轨迹 ,当 e > 1 时,是双曲线 .当 00) (2) 开口向左 y2 = -2px (p>0)(3) 开口向上 x2 = 2py (p>0) (4) 开口向下 x2 = -2py (p>0)第八章圆锥曲线方程就标准方程而言,椭圆、双曲线有两个参数,而抛物线只有一个参数。方程图形准线焦点焦半径)0(22ppxy)0(22ppxy)0(22ppyx)0(22ppyx)0,( 2pF)0,(2pF ),0(2pF),0(2pF2px2px 2yp2py lFyxOlFyxOlFyxOlFyxO02px02px02py02py抛物线的标准方程各对应的焦点弦的长度如何表示 ?( 三 ) 抛物线 y2 =2px ( p>0 )的固有性质2). 顶点 , 焦点在对称轴上探究?3). 准线垂直于对称轴yox)0,2( pF抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;1) 、范围:xyOAFBy2=2px2p过焦点而垂直于对称轴的弦AB ,称为抛物线的通径,pp ,2 pp ,2|AB|=2p:).4的几何意义p焦点到准线的距离:2pp ( 1 )已知点 A ( -2 , 3 )与抛物线 的焦点的距离是 5 ,则 P = 。 22(0)ypx p( 2 )抛物线 的弦 AB 垂直 x 轴,若 |AB|= , 则焦点到 AB 的距离为 。 24yx4 342( 3 )已知直线 x-y=2 与抛物线 交于 A 、 B 两 点,那么线段 AB 的中点坐标是 。24yx(4,2)课堂练习(4). 抛物线y=ax2 的准线方程是 y=2 ,则 a 的值为( ) A. 1/8 B. -1/8 C. 8 D. -8B2 、如果抛物线 C : y2=a(x+1)(1) 若 C 的准线方程为 x=-3 ,那么该抛物线的焦点坐标为 ( )A ) (1,0) B) (2,0) C(3,0) D) (-1,0)(2) 若 a>0 ,直线 L 过 C 的焦点,并且与C 的对称轴垂直,若 L 被 C 截得的弦长为 4, 则 a=_______4课堂练习例 1. 已知抛物线顶点在原点,焦点在坐标轴上, 又知此抛物线上的一点A(m,-3) 到焦点 F 的距离为 5 ,求m 的值,并写出此抛物线的方程解题分析 : 虽然抛物线顶点在原点 , 焦点在坐标轴上 , 处于标准位置 , 然而方向并不确定 , 从点 A(m, -3) 在直线 y=-3 上看 ...