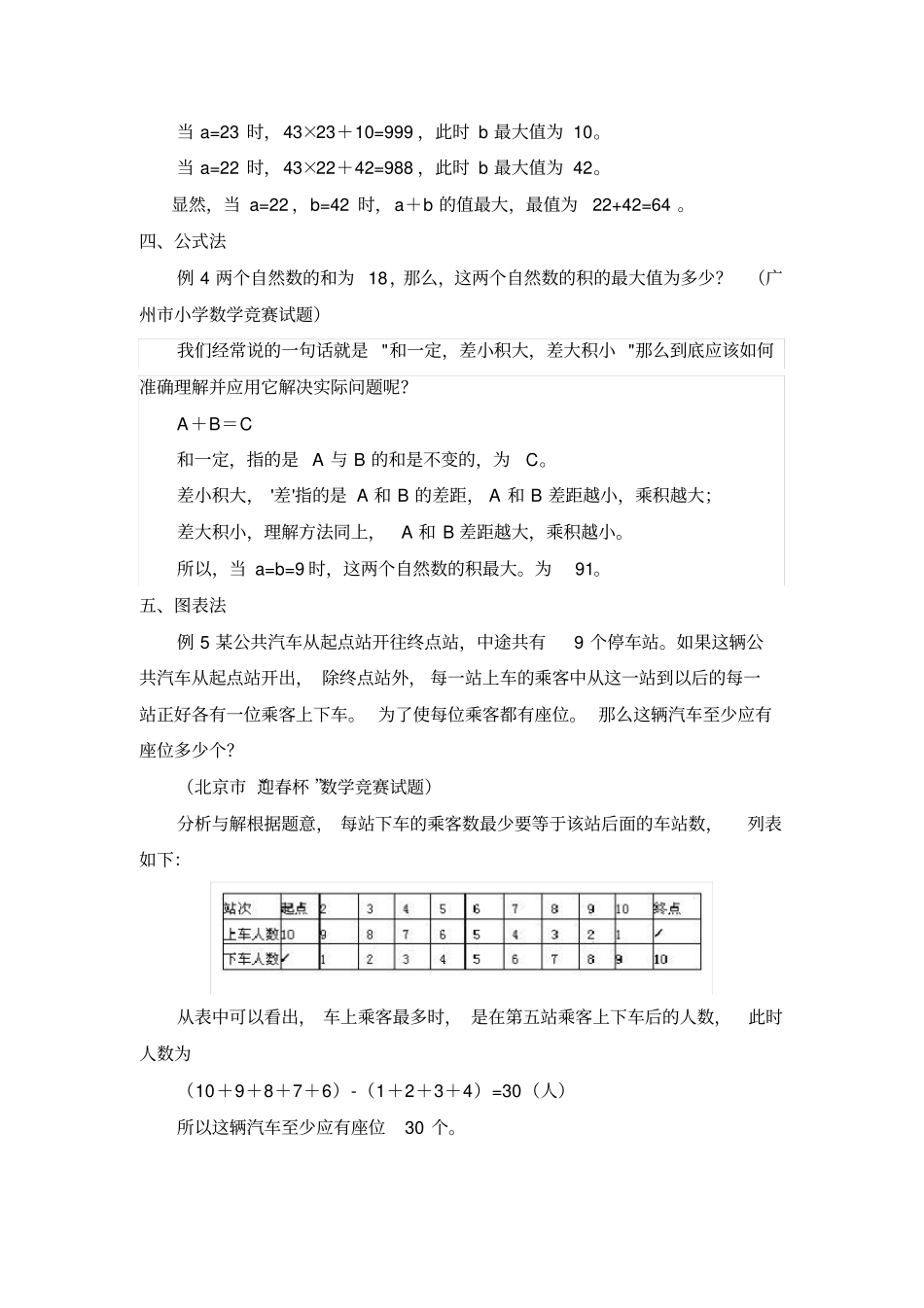
四年级奥数之最值问题知识点睛: 在一定范围内求最大值或最小值的问题,我们称之为“最大最小问题 ”。“最大 ”、“最小”是我们所熟悉的两个概念,多年来各级数学竞赛中经常会出现求最值问题,解决办法有:一、枚举法例 1 一把钥匙只能开一把锁,现在有4 把钥匙 4 把锁。但不知哪把钥匙开哪把锁,最多要试多少次就能配好全部的钥匙和锁?(北京市第三届 “迎春杯 ”数学竞赛试题)分析与解开第一把锁,按最坏情况考虑试了3 把还未成功,则第4 把不用试了,它一定能打开这把锁,因此需要3 次。同样的道理开第二把锁最多试2次,开第三把锁最多试1 次,最后一把锁则不用再试了。 这样最多要试的次数为:3+2+1=6(次)。二、综合法例 2x3=84A (x、A 均为自然数)。 A 的最小值是 ______ 。(1997 年南通市数学通讯赛试题)分析与解根据题意, 84A 开立方的结果应为自然数,于是我们可以把84 分解质因数,得 84=2×2×3×7,因此 x3=2×2×3×7×A,其中 A 的质因数至少含有一个 2、两个 3、两个 7,才能满足上述要求。即 A 的最小值为( 2×3×3×7×7=)882 。三、分析法例 3 一个三位数除以 43,商是 a,余数是 b,(a、b 均为自然数), a+b的最大值是多少?(广州市五年级数学竞赛试题)分析与解若要求 a+b 的最大值,我们只要保证在符合题意之下,a、b 尽可能大。由乘除法关系得43a+b=一个三位数因为 b 是余数,它必须比除数小,即b<43b 的最大值可取 42。根据上面式子,考虑到a 不能超过 23。(因为 24×43>1000 ,并不是一个三位数)当 a=23 时,43×23+10=999 ,此时 b 最大值为 10。当 a=22 时,43×22+42=988 ,此时 b 最大值为 42。显然,当 a=22 ,b=42 时,a+b 的值最大,最值为22+42=64 。四、公式法例 4 两个自然数的和为 18,那么,这两个自然数的积的最大值为多少?(广州市小学数学竞赛试题)我们经常说的一句话就是 "和一定,差小积大,差大积小 "那么到底应该如何准确理解并应用它解决实际问题呢?A+B=C 和一定,指的是 A 与 B 的和是不变的,为C。差小积大, '差'指的是 A 和 B 的差距, A 和 B 差距越小,乘积越大;差大积小,理解方法同上,A 和 B 差距越大,乘积越小。所以,当 a=b=9 时,这两个自然数的积最大。为91。五、图表法例 5 某公共汽车从起点站开往终点站,中途共有9 个停车站。如果这辆公共汽...