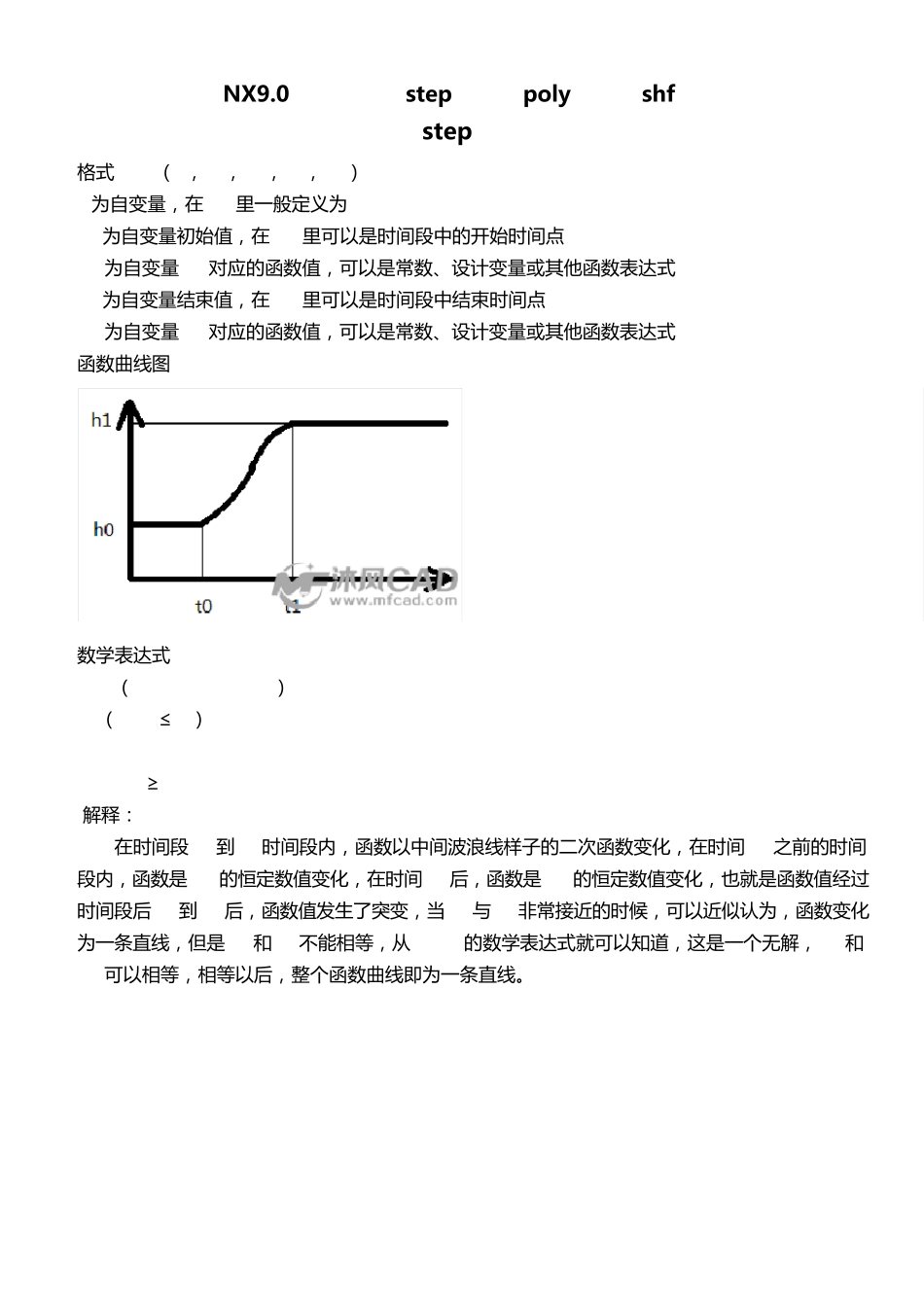
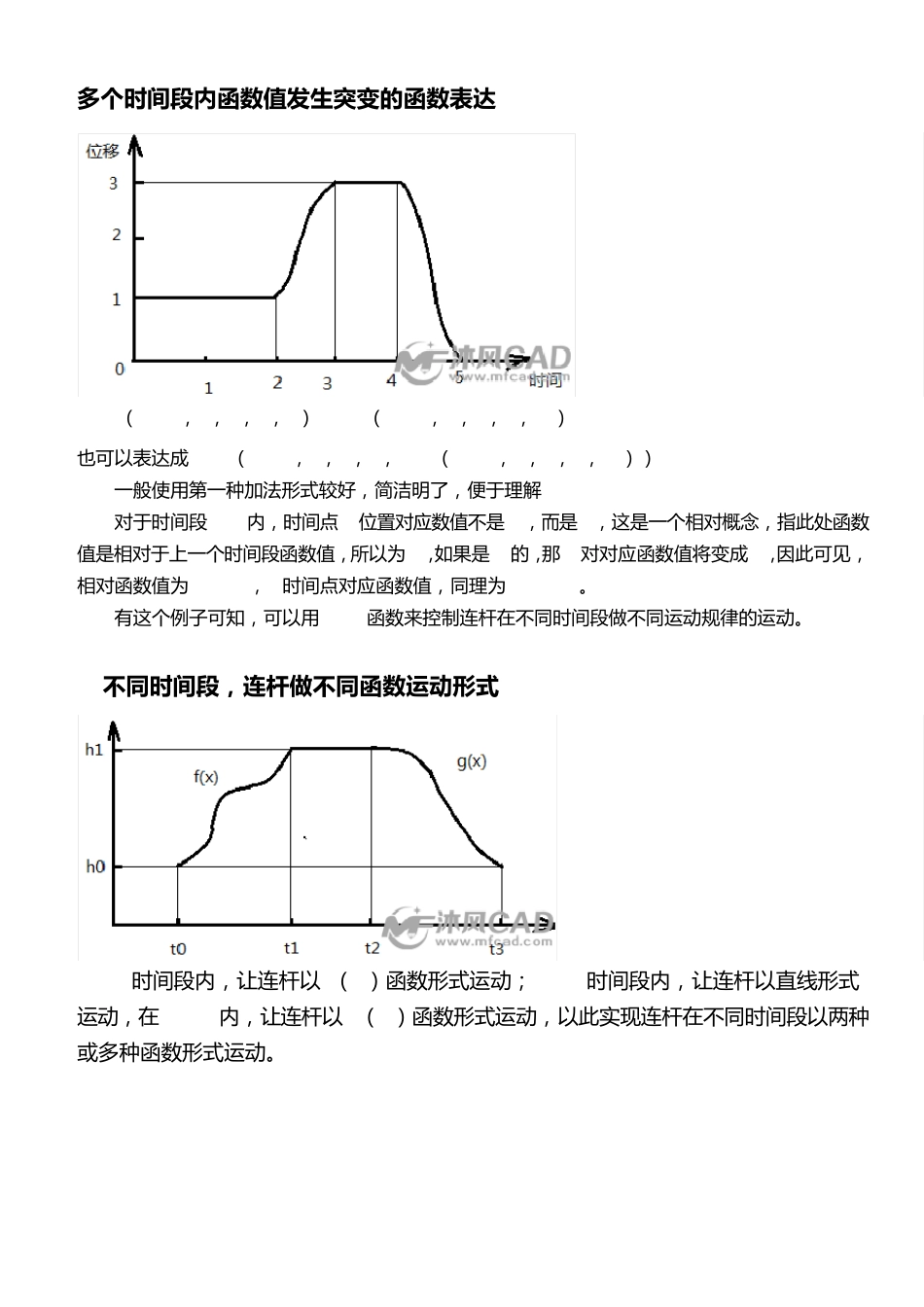
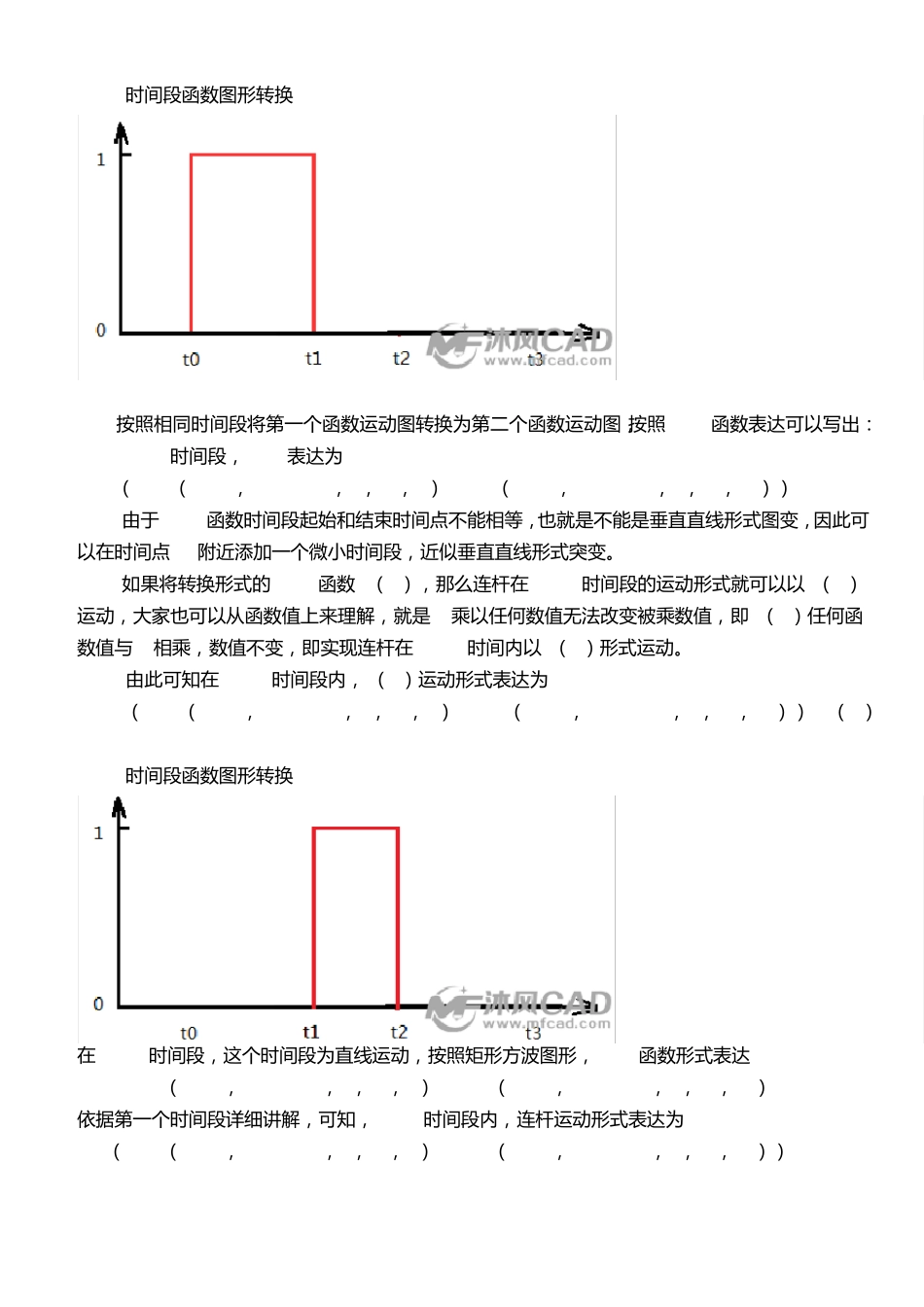
NX9.0 运动仿真—step 函数、poly 涵式、shf 函数 step 函数 格 式 step( x, x0, h0, x1, h1) x为 自 变 量 , 在 ug里 一 般 定 义 为 time x0为 自 变 量 初 始 值 , 在 ug里 可 以 是 时 间 段 中 的 开 始 时 间 点 h0为 自 变 量 x0对 应 的 函 数 值 , 可 以 是 常 数 、设 计 变 量 或 其 他 函 数 表 达 式 x1为 自 变 量 结 束 值 , 在 ug里 可 以 是 时 间 段 中 结 束 时 间 点 h1为 自 变 量 x1对 应 的 函 数 值 , 可 以 是 常 数 、设 计 变 量 或 其 他 函 数 表 达 式 函 数 曲 线 图 数 学 表 达 式 step( time,t0,h0,t1,h1) = h0( time≤t0) h0+(( time-t0)/(t1-t0))2*(h1-h2) h1(time≥t1) 解 释 : 在 时 间 段 t0到 t1时 间 段 内 , 函 数 以 中 间 波 浪 线 样 子 的 二 次 函 数 变 化 , 在 时 间t0之 前 的 时 间段 内 , 函 数 是 h0的 恒 定 数 值 变 化 , 在 时 间 t1后 , 函 数 是 h1的 恒 定 数 值 变 化 , 也 就 是 函 数 值 经 过时 间 段 后 t0到 t1后 , 函 数 值 发 生 了 突 变 , 当 t0与 t1非 常 接 近 的 时 候 , 可 以 近 似 认 为 , 函 数 变 化为 一 条 直 线 , 但 是t0和 t1不 能 相 等 , 从 t0-t1的 数 学 表 达 式 就 可 以 知 道 , 这 是 一 个 无 解 , h0和h1可 以 相 等 , 相 等 以 后 , 整 个 函 数 曲 线 即 为 一 条 直 线 。 多 个 时 间 段 内 函 数 值 发 生 突 变 的 函 数 表 达 step( time, 2, 1, 3, 3) +step( time, 4, 0, 5, -3) 也 可 以 表 达 成 step( time, 2, 1, 3, step( time, 4, 0, 5, -3) ) 一 般 使 用 第 一 种 加 法 形 式 较 好 , 简 洁 明 了 , 便 于 理 解 对 于 时 间 段 4-5内 , 时 间 点 4位 置 对 应 数 值 不 是3, 而 是 0, 这 是 一 个 相 对 概 念 , 指 此 处 函 数值 是 相 对 于 上 一 个 时 间 段 函 数 值 , 所 以 为 0, 如...