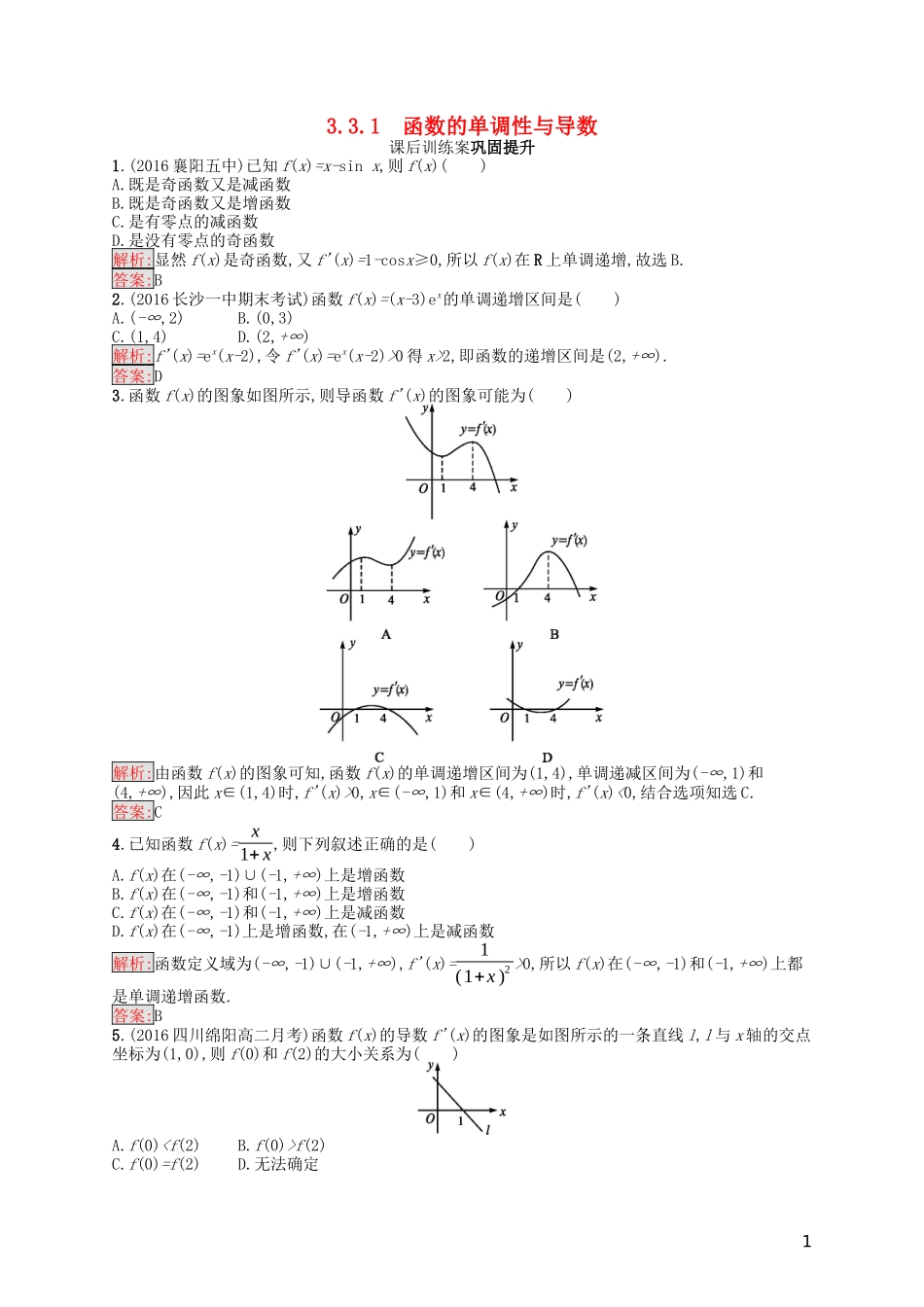
3.3.1 函数的单调性与导数课后训练案巩固提升1.(2016 襄阳五中)已知 f(x)=x-sin x,则 f(x)( )A.既是奇函数又是减函数B.既是奇函数又是增函数C.是有零点的减函数D.是没有零点的奇函数解析:显然 f(x)是奇函数,又 f'(x)=1-cosx≥0,所以 f(x)在 R 上单调递增,故选 B.答案:B2.(2016 长沙一中期末考试)函数 f(x)=(x-3)ex的单调递增区间是( )A.(-∞,2)B.(0,3)C.(1,4)D.(2,+∞)解析:f'(x)=ex(x-2),令 f'(x)=ex(x-2)>0 得 x>2,即函数的递增区间是(2,+∞).答案:D3.函数 f(x)的图象如图所示,则导函数 f'(x)的图象可能为( )解析:由函数 f(x)的图象可知,函数 f(x)的单调递增区间为(1,4),单调递减区间为(-∞,1)和(4,+∞),因此 x∈(1,4)时,f'(x)>0,x∈(-∞,1)和 x∈(4,+∞)时,f'(x)<0,结合选项知选 C.答案:C4.已知函数 f(x)= x1+ x,则下列叙述正确的是( )A.f(x)在(-∞,-1)∪(-1,+∞)上是增函数B.f(x)在(-∞,-1)和(-1,+∞)上是增函数C.f(x)在(-∞,-1)和(-1,+∞)上是减函数D.f(x)在(-∞,-1)上是增函数,在(-1,+∞)上是减函数解析:函数定义域为(-∞,-1)∪(-1,+∞),f'(x)=1(1+x )2 >0,所以 f(x)在(-∞,-1)和(-1,+∞)上都是单调递增函数.答案:B5.(2016 四川绵阳高二月考)函数 f(x)的导数 f'(x)的图象是如图所示的一条直线 l,l 与 x 轴的交点坐标为(1,0),则 f(0)和 f(2)的大小关系为( )A.f(0)f(2)C.f(0)=f(2)D.无法确定1解析:由图知 f'(1)=0;当 x<1 时,f'(x)>0,函数 f(x)单调递增;当 x>1 时,f'(x)<0,函数 f(x)单调递减.又因为 f(x)的导数 f'(x)的图象是如题图所示的一条直线 l,所以 f(x)是以 x=1 为对称轴且开口向下的抛物线,故 f(0)=f(2).答案:C6.(2016 长沙一中期末考试)如图所示的是函数 y=f(x)的导函数 y=f'(x)的图象,则在(-2,5)上函数y=f(x)的单调递增区间为 . 解析:由 f'(x)的图象可知,当 x∈(-1,2)和 x∈(4,5)时,f'(x)>0,故函数 f(x)在(-1,2)和(4,5)上都是单调递增函数.答案:(-1,2)和(4,5)7.函数 y= ex2x 的单调递减区间是 . 解析:函数定义域为(-∞,0)∪(0,+∞),y'= xex -ex2x2=ex( x-1)2x2,令 y'<0,得 x<1,且 x≠0,故函数递减区间是(-∞,0)和(0,1).答案:(-∞,0)和(0,1)8.若函数 f(x)图象上任意一点(x0,f(x0))处的切线斜率 k=ln x0-2,则 f(x)的单调递增区间是 . 解析:由题意得 f'(x)=lnx-2,令 f'(x)=lnx-2>0,得 x>e2,所以 f(x)的单调递增区间是(e2,+∞).答案...