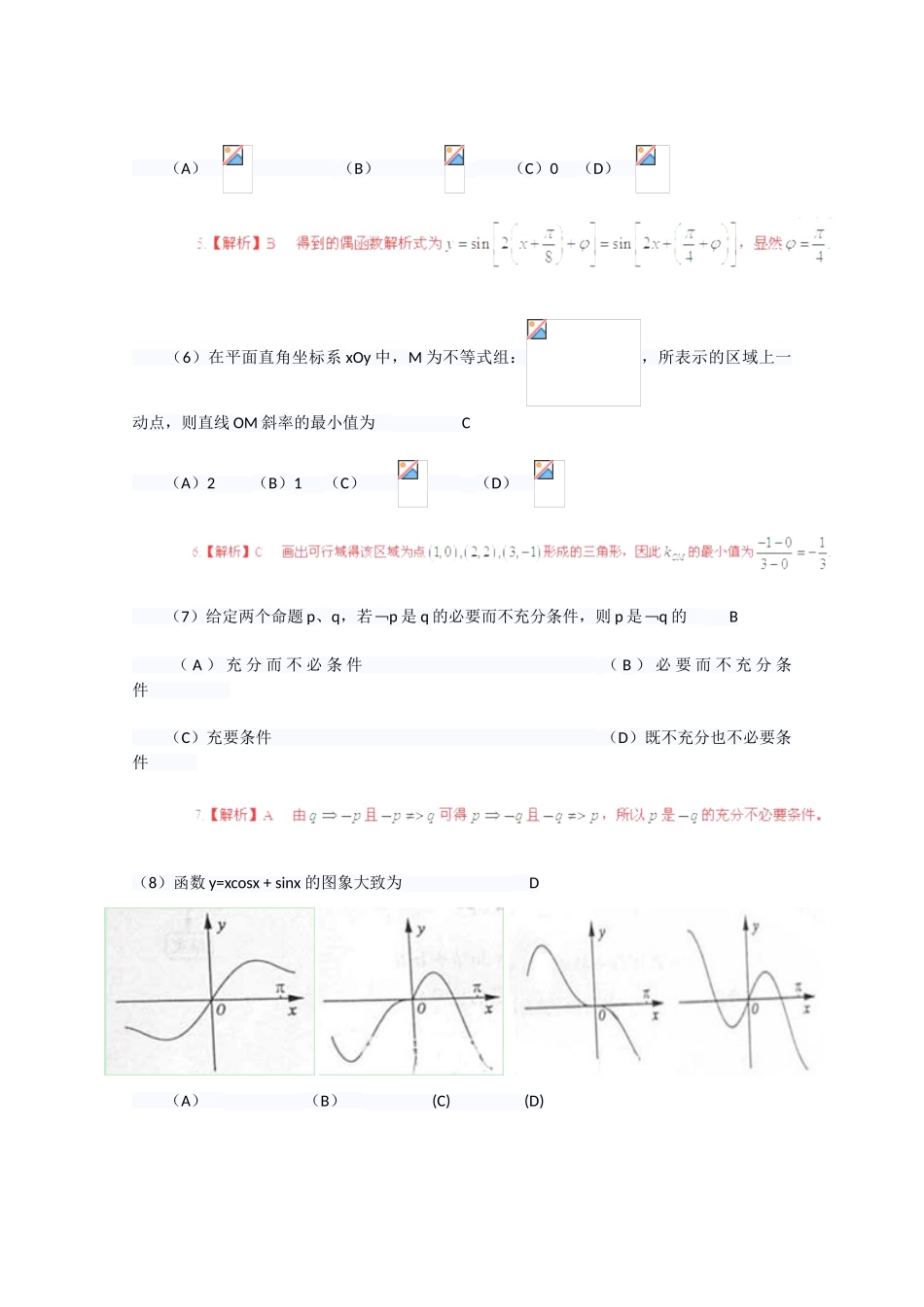
2024 年山东高考数学试题一、选择题:本大题共 12 小题,每小题 5 分,满分 60 分.在每小题给出的四个选项中,只有一项是符合题目要求的。 (1)复数 z 满足(z-3)(2-i)=5(i 为虚数单位),则 z 的共轭复数为( D ) A. 2+i B.2-i C. 5+i D.5-i (2)设集合 A={0,1,2},则集合 B={x-y |x∈A, y∈A }中元素的个数是( C ) A. 1 B. 3 C. 5 D.9 (3)已知函数 f(x)为奇函数,且当 x>0 时, f(x) =x2+ ,则 f(-1)= ( A ) (A)-2 (B)0 (C)1 (D)2 (4)已知三棱柱 ABC-A1B1C1 的侧棱与底面垂直,体积为 ,底面积是边长为 的正 三角形,若 P 为底面 A1B1C1的中心,则 PA 与平面 ABC 所成角的大小为 ( B ) (A) (B) (C) (D) (5)将函数 y=sin(2x +)的图像沿 x 轴向左平移 个单位后,得到一个偶函数的图像,则的一个可能取值为 B (A) (B) (C)0 (D) (6)在平面直角坐标系 xOy 中,M 为不等式组:,所表示的区域上一动点,则直线 OM 斜率的最小值为 C (A)2 (B)1 (C) (D) (7)给定两个命题 p、q,若﹁p 是 q 的必要而不充分条件,则 p 是﹁q 的 B ( A ) 充 分 而 不 必 条 件 ( B ) 必 要 而 不 充 分 条件 (C)充要条件 (D)既不充分也不必要条件 (8)函数 y=xcosx + sinx 的图象大致为 D (A) (B) (C) (D) (9)过点(3,1)作圆(x-1)2+y2=1 的两条切线,切点分别为 A,B,则直线 AB 的方程为 A (A)2x+y-3=0 (B)2x-y-3=0 (C)4x-y-3=0 (D)4x+y-3=0 (10)用 0,1,…,9 十个数字,可以组成有重复数字的三位数的个数为 B (A)243 (B)252 (C)261 (D)279 (11)抛物线 C1:y= x2(p>0)的焦点与双曲线 C2: 的右焦点的连线交 C1于第一象限的点 M.若 C1在点 M 处的切线平行于 C2的一条渐近线,则 p= D (12)设正实数 x,y,z 满足 x2-3xy+4y2-z=0.则当取得最大值时,的最大值为 B (A)0 (B)1 (C) (D)3 二、填空题:本大题共 4 小题,每小题 4 分,共 16 分 (13)执行右面的程序框图,若输入的的值为 0.25,则输入的 n 的值为 3 (14)在区间[-3,3]上随机取一个数 x,使得 |x+1 |- |x-2 |≥1 成立的概率为 (15)已知向量与的夹角为,且若且,则实数的值为 (16)定义“正对数”:,现有四个命题:...