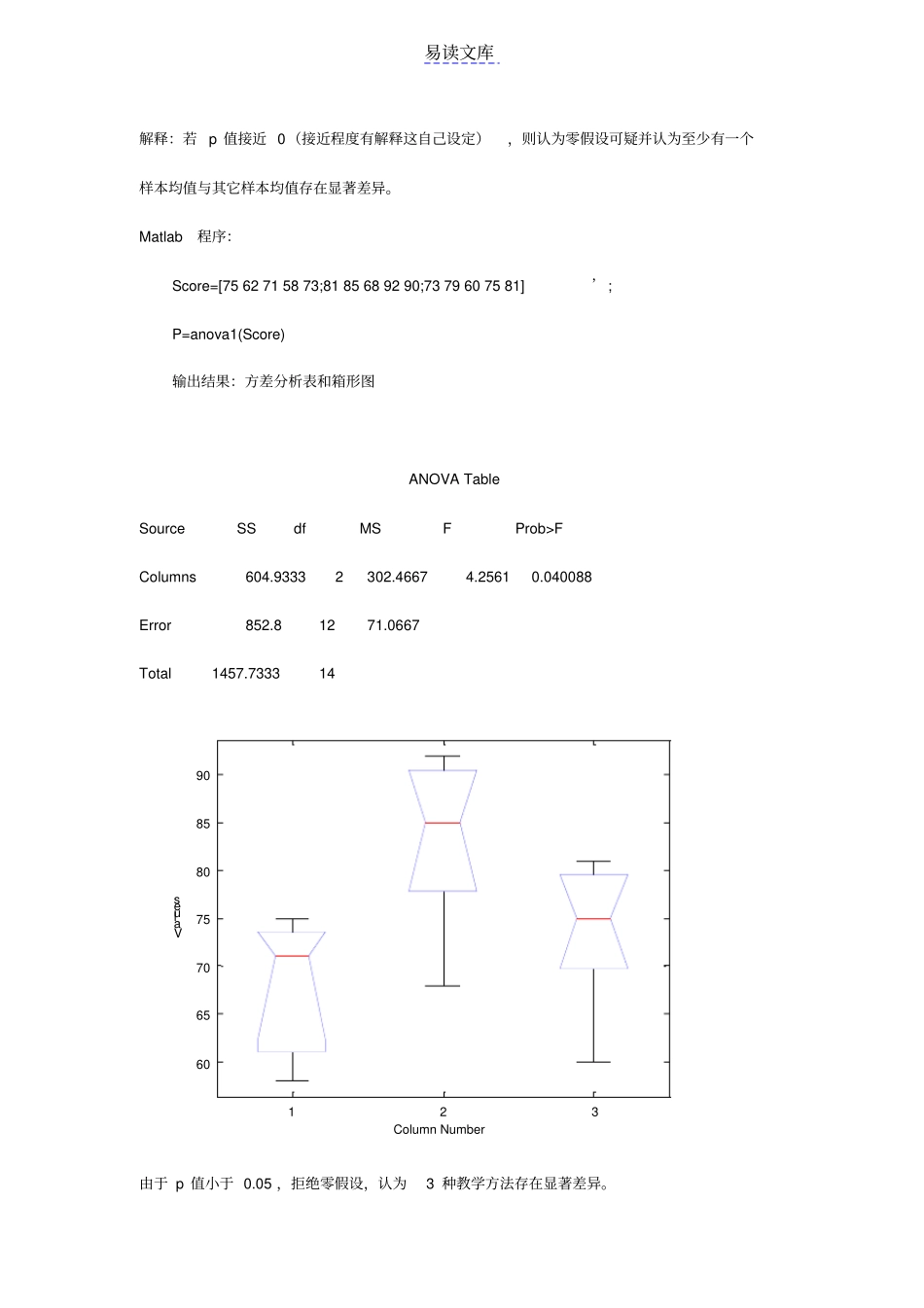
易读文库一 Matlab作方差分析方差分析是分析试验 (或观测) 数据的一种统计方法。 在工农业生产和科学研究中,经常要分析各种因素及因素之间的交互作用对研究对象某些指标值的影响。在方差分析中,把试验数据的总波动(总变差或总方差)分解为由所考虑因素引起的波动(各因素的变差)和随机因素引起的波动(误差的变差),然后通过分析比较这些变差来推断哪些因素对所考察指标的影响是显著的,哪些是不显著的。【例 1 】(单因素方差分析)一位教师想要检查3 种不同的教学方法的效果,为此随机地选取水平相当的15 位学生。把他们分为3 组,每组 5 人,每一组用一种方法教学,一段时间以后,这位教师给15 位学生进行统考,成绩见下表1。问这 3 种教学方法的效果有没有显著差异。表 1 学生统考成绩表方法成绩甲75 62 71 58 73 乙71 85 68 92 90 丙73 79 60 75 81 Matlab中可用函数anova1( ⋯)函数进行单因子方差分析。调用格式: p=anova1(X) 含义:比较样本m ×n 的矩阵 X 中两列或多列数据的均值。其中,每一列表示一个具有m个相互独立测量的独立样本。返回:它返回X 中所有样本取自同一总体(或者取自均值相等的不同总体)的零假设成立的概率 p 。易读文库解释:若 p 值接近 0(接近程度有解释这自己设定),则认为零假设可疑并认为至少有一个样本均值与其它样本均值存在显著差异。Matlab程序:Score=[75 62 71 58 73;81 85 68 92 90;73 79 60 75 81]’; P=anova1(Score) 输出结果:方差分析表和箱形图ANOVA Table Source SS df MS F Prob>F Columns 604.9333 2 302.4667 4.2561 0.040088Error 852.8 12 71.0667 Total 1457.7333 14 12360657075808590ValuesColumn Number由于 p 值小于 0.05 ,拒绝零假设,认为3 种教学方法存在显著差异。易读文库例 2(双因素方差分析) 为了考察 4 种不同燃料与3 种不同型号的推进器对火箭射程(单位:海里)的影响,做了12 次试验,得数据如表2 所示。表 2 燃料 -推进器 -射程数据表推进器 1 推进器 2 推进器 3 燃料 1 58.2 56.2 65.3 燃料 2 49.1 54.1 51.6 燃料 3 60.1 70.9 39.2 燃料 4 75.8 58.2 48.7 在 Matlab中利用函数anova2函数进行双因素方差分析。调用格式: p=anova2(X,reps) 含义:比较样本X 中两列或两列以上和两行或两行以上数据的均值。不同列的数据代表因...