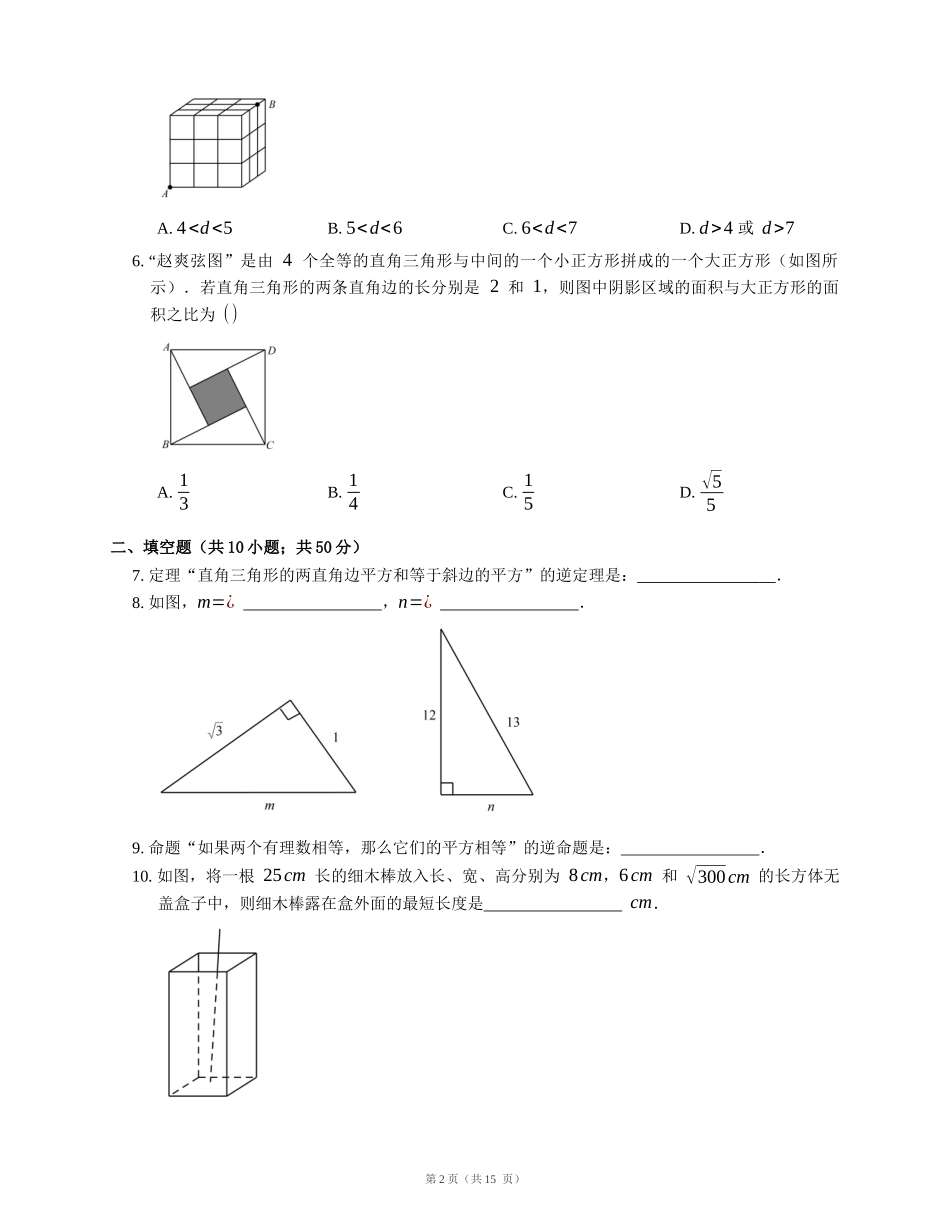
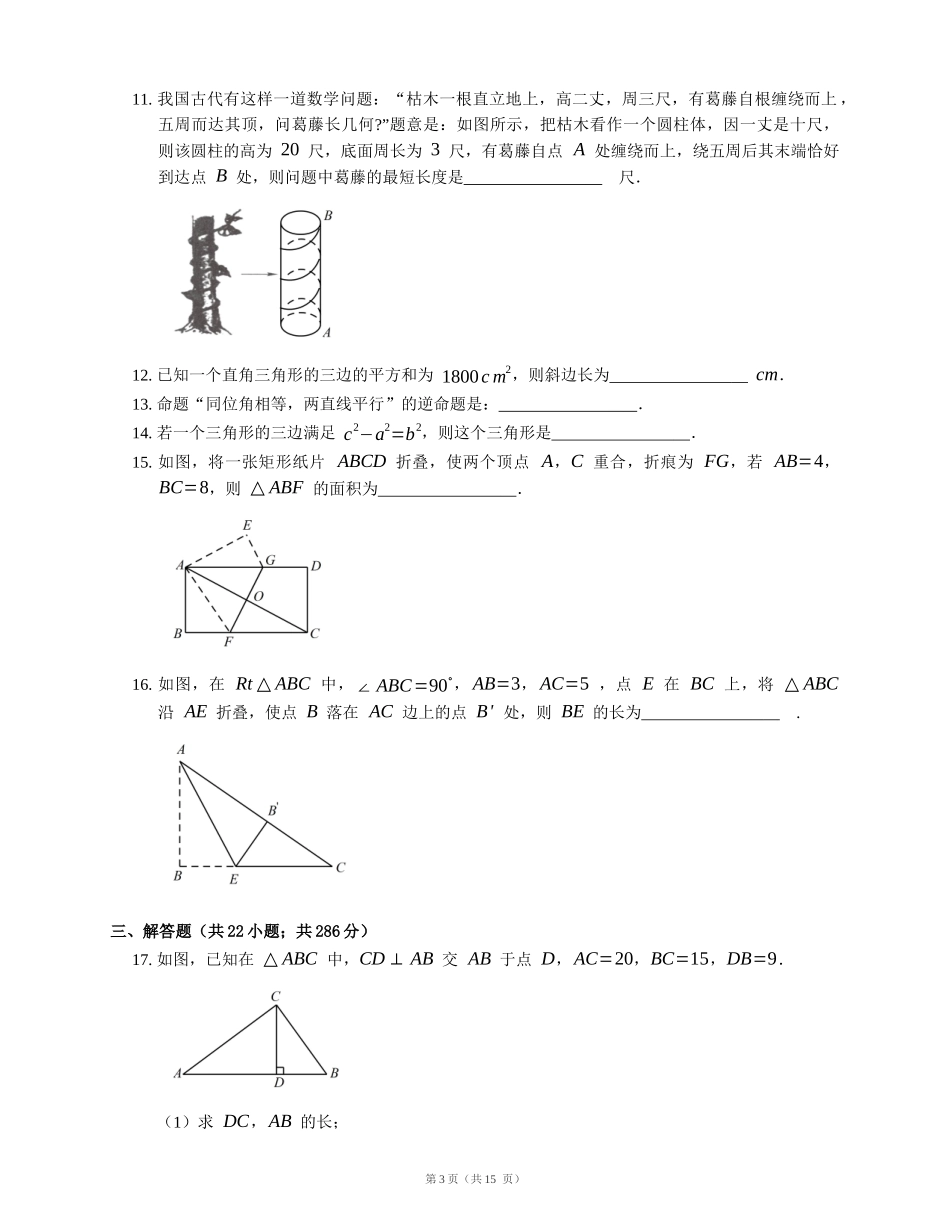
勾股定理习题巩固一、选择题(共6小题;共30分)1.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为()A.12mB.13mC.16mD.17m2.下列四组线段中,能组成直角三角形的是()A.a=1,b=2,c=3B.a=2,b=3,c=4C.a=2,b=4,c=5D.a=3,b=4,c=53.如图,点A为正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是()A.3B.√2+2C.√10D.44.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A.5√21B.25C.10√5+5D.355.如图所示是一棱长为3的正方体,把它分成3×3×3个小正方体,每个小正方体的边长都是1.如果一只蚂蚁从点A爬到点B,那么A,B间的最短距离d满足()第1页(共15页)A.44或d>76.“赵爽弦图”是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形的两条直角边的长分别是2和1,则图中阴影区域的面积与大正方形的面积之比为()A.13B.14C.15D.√55二、填空题(共10小题;共50分)7.定理“直角三角形的两直角边平方和等于斜边的平方”的逆定理是:.8.如图,m=¿,n=¿.9.命题“如果两个有理数相等,那么它们的平方相等”的逆命题是:.10.如图,将一根25cm长的细木棒放入长、宽、高分别为8cm,6cm和√300cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是cm.第2页(共15页)11.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是尺.12.已知一个直角三角形的三边的平方和为1800cm2,则斜边长为cm.13.命题“同位角相等,两直线平行”的逆命题是:.14.若一个三角形的三边满足c2−a2=b2,则这个三角形是.15.如图,将一张矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG,若AB=4,BC=8,则△ABF的面积为.16.如图,在Rt△ABC中,∠ABC=90∘,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点Bʹ处,则BE的长为.三、解答题(共22小题;共286分)17.如图,已知在△ABC中,CD⊥AB交AB于点D,AC=20,BC=15,DB=9.(1)求DC,AB的长;第3页(共15页)(2)求证:△ABC是直角三角形.18.有一圆柱体高为8cm,底面圆的半径为2cm,如图,在AA1上的点Q处有一只蜘蛛,QA1=3cm,在BB1上的点P处有一只苍蝇,PB=2cm.蜘蛛要从点Q处沿圆柱体表面去吃点P处的苍蝇,求蜘蛛爬行的最短路径长.(π取3)19.如图一只蚂蚁要从正方体的一个顶点A爬一个顶点B,如果正方体棱是2,求最短的路线长.20.如图,在△ABC中,AC=5,BC=12,AB=13,D是BC的中点,求AD的长和△ABD的面积.21.如图,地上有一圆柱,在圆柱下底面的A点处有一蚂蚁,它想沿圆柱表面爬行,吃到上底面上与A点相对的B点处的食物(π的近似值取3,下同).(1)当圆柱的高h=12厘米,底面半径r=3厘米时,蚂蚁沿侧面爬行时最短路程是多少?(2)当圆柱的高h=3厘米,底面半径r=3厘米时,蚂蚁沿侧面爬行时也可沿AC到上底面爬行,最短路程是多少?(3)探究:当圆柱的高为h,圆柱底面半径为r时,蚂蚁怎样爬行的路程最短?路程最短为多少?第4页(共15页)22.一只蚂蚁从长、宽都是30cm,高是80cm的长方体纸箱的A点沿纸箱爬到B点,如图,求它爬行的最短路线的长.23.如图,将长方形纸片ABCD的一边AD向下折叠,点D落在BC边上的点F处.已知AB=CD=8cm,BC=AD=10cm,求EC的长.24.如图,铁路上A,B两站(视为直线上两点)相距25km,有C,D两个村庄(视为两个点),DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在铁路AB旁建一个土特产收购站E,使得C,D两村到收购站的距离相等,那么收购站应建在离A站多远处?25.如图,某工厂A前有一条笔直的公路,从工厂A原有的两...