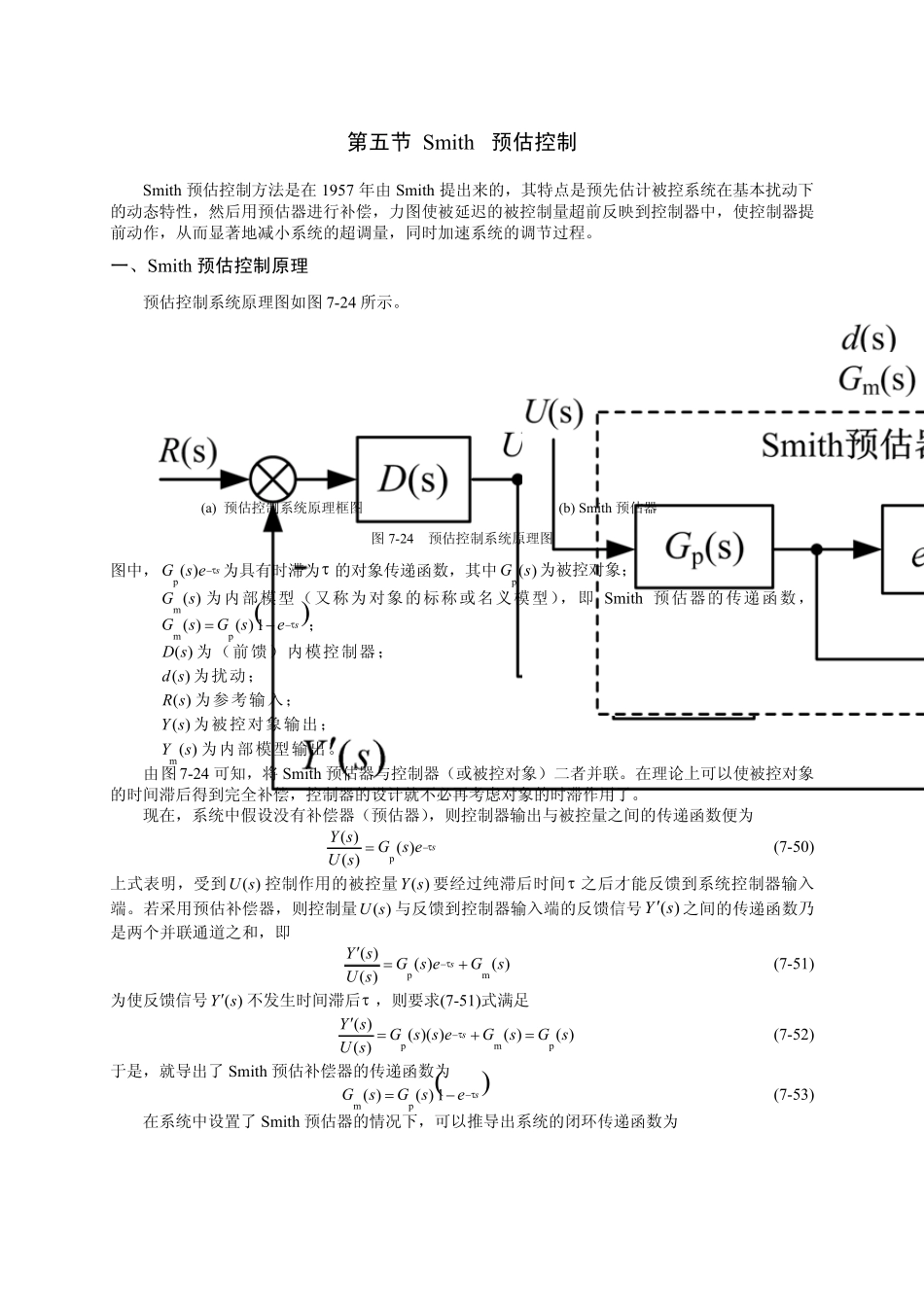
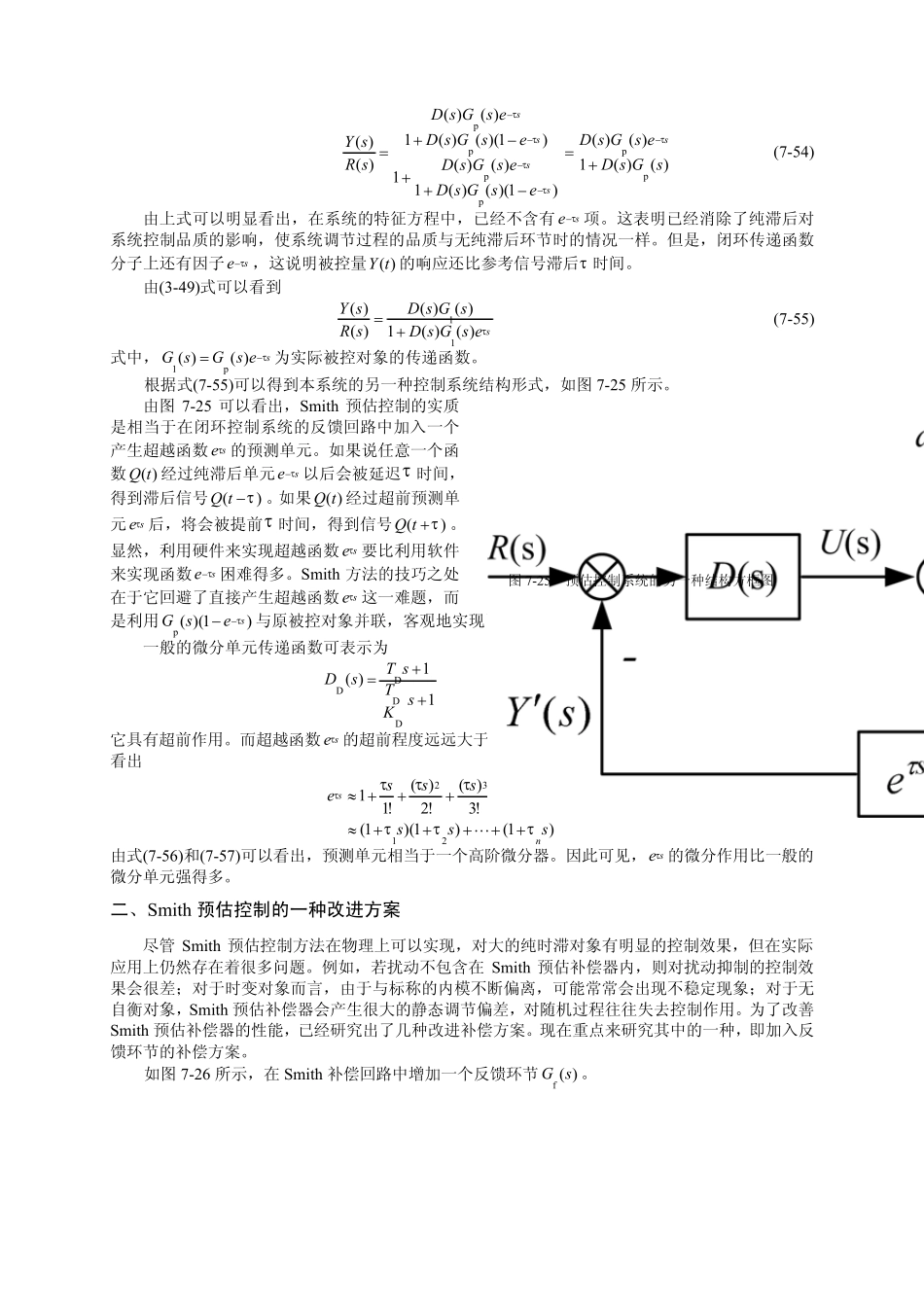
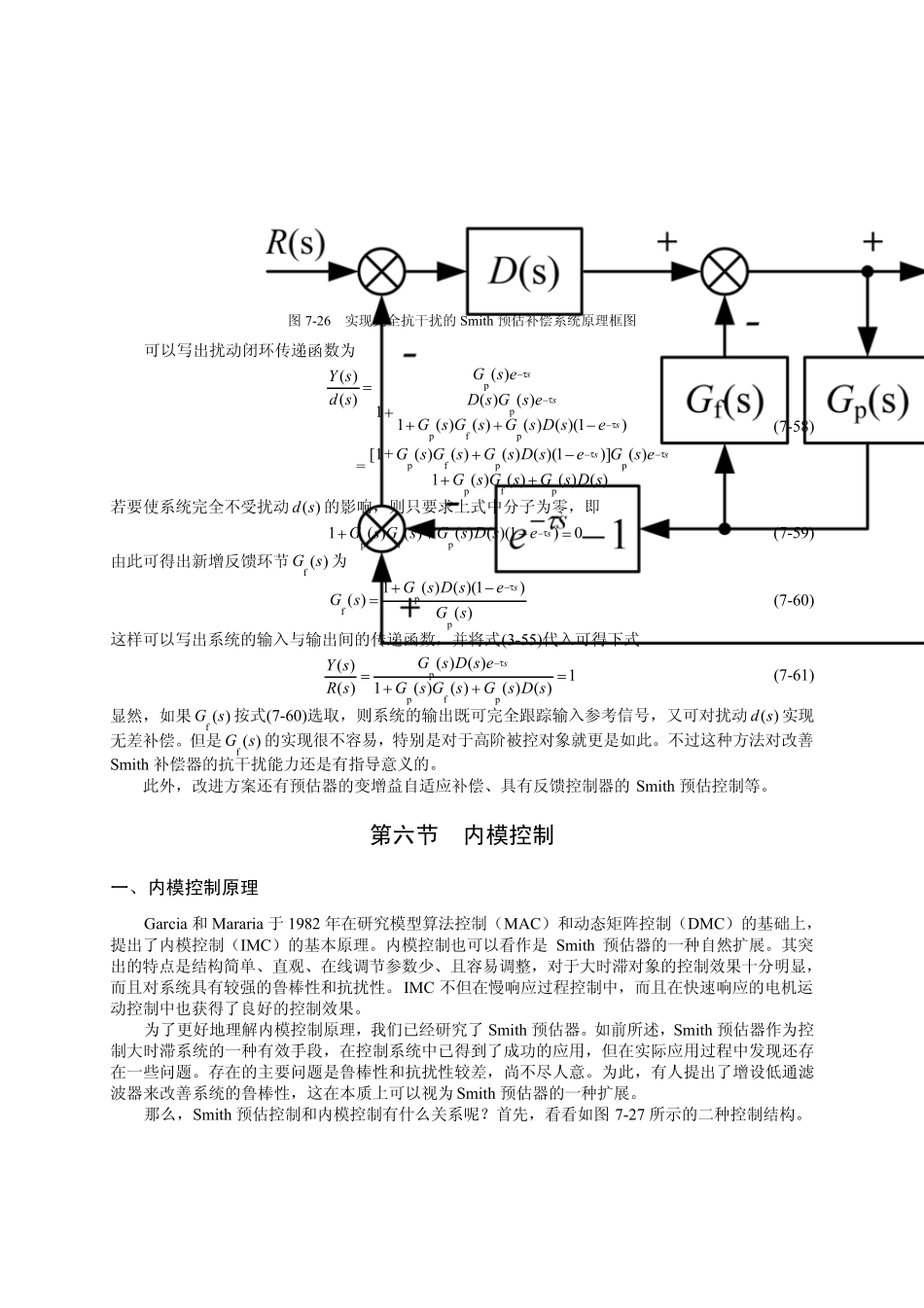
第五节 Smith 预估控制 Smith 预估控制方法是在1957 年由Smith 提出来的,其特点是预先估计被控系统在基本扰动下的动态特性,然后用预估器进行补偿,力图使被延迟的被控制量超前反映到控制器中,使控制器提前动作,从而显著地减小系统的超调量,同时加速系统的调节过程。 一、Smith 预估控制原理 预估控制系统原理图如图7-24 所示。 (a) 预估控制系统原理框图 (b) Smith 预估器 图7-24 预估控制系统原理图 图中,sesGτ−)(p为具有时滞为τ 的对象传递函数,其中)(p sG为被控对象; )(m sG为内部模型(又称为对象的标称或名义模型),即 Smith 预估器的传递函数,()sesGsGτ−−=1)()(pm; )(sD为(前馈)内模控制器; )(sd为扰动; )(sR为参考输入; )(sY为被控对象输出; )(m sY为内部模型输出。 由图7-24 可知,将 Smith 预估器与控制器(或被控对象)二者并联。在理论上可以使被控对象的时间滞后得到完全补偿,控制器的设计就不必再考虑对象的时滞作用了。 现在,系统中假设没有补偿器(预估器),则控制器输出与被控量之间的传递函数便为 sesGsUsYτ−=)()()(p (7-50) 上式表明,受到)(sU控制作用的被控量)(sY要经过纯滞后时间τ 之后才能反馈到系统控制器输入端。若采用预估补偿器,则控制量)(sU与反馈到控制器输入端的反馈信号)(sY ′之间的传递函数乃是两个并联通道之和,即 )()()()(mpsGesGsUsYs +=′−τ (7-51) 为使反馈信号)(sY′不发生时间滞后τ ,则要求(7-51)式满足 )()())(()()(pmpsGsGessGsUsYs=+=′−τ (7-52) 于是,就导出了 Smith 预估补偿器的传递函数为 ()sesGsGτ−−=1)()(pm (7-53) 在系统中设置了 Smith 预估器的情况下,可以推导出系统的闭环传递函数为 )()(1)()()1)(()(1)()(1)1)(()(1)()()()(ppppppsGsDesGsDesGsDesGsDesGsDesGsDsRsYsssss+=−++−+=−−−−−τττττ (7-54) 由上式可以明显看出,在系统的特征方程中,已经不含有se τ− 项。这表明已经消除了纯滞后对系统控制品质的影响,使系统调节过程的品质与无纯滞后环节时的情况一样。但是,闭环传递函数分子上还有因子se τ− ,这说明被控量)(tY的响应还比参考信号滞后τ 时间。 由(3-49)式可以看到 sesGsDsGsDsRsYτ)()(1)()()()(11+= (7-55) 式中,sesGsGτ−=)()(p1为实际被控对象的传递函数。 根据式(7-55)可以得到本系统的另一种控制系统结构形式,如图 7-25 所示。 由...