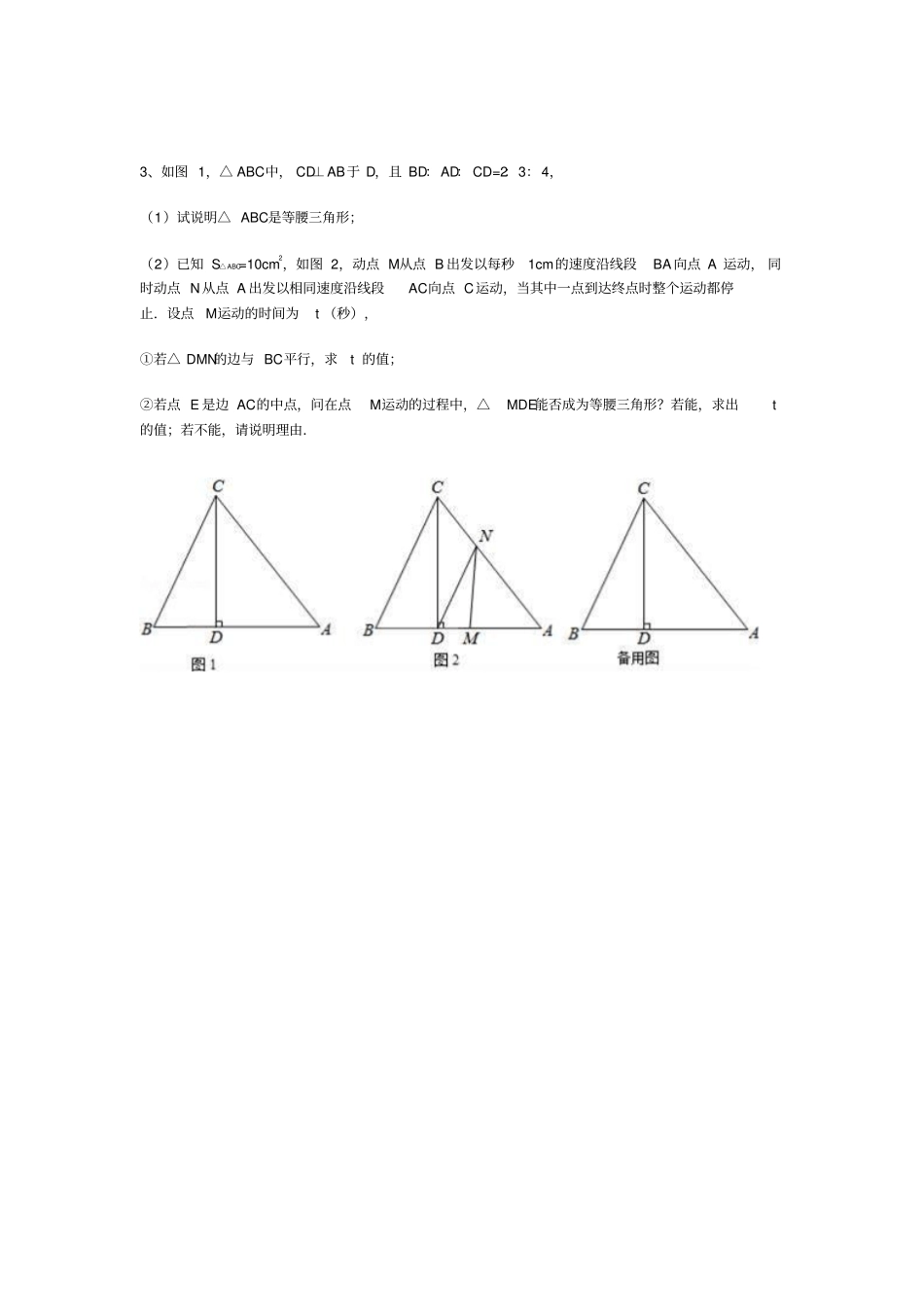
勾股定理竞赛培训题1、如图 1,△ ABC和△ CDE都是等腰直角三角形,∠C=90° ,将△ CDE绕点 C 逆时针旋转一个角度α ( 0° < α <90° ),使点A,D,E在同一直线上,连接AD,BE.(1)①依题意补全图2;②求证: AD=BE,且 AD⊥BE;③作 CM⊥DE,垂足为M,请用等式表示出线段CM, AE,BE之间的数量关系;(2)如图 3,正方形ABCD边长为,若点 P 满足 PD=1,且∠ BPD=90° ,请直接写出点A到 BP的距离.2、( 1)问题发现:如图1,△ ACB和△ DCE均为等边三角形,当△DCE旋转至点 A,D,E 在同一直线上,连接BE,易证△ BCE≌△ ACD.则①∠ BEC=______° ;②线段AD、BE之间的数量关系是______.(2)拓展研究:如图 2,△ ACB和△ DCE均为等腰三角形,且∠ACB=∠ DCE=90° ,点 A、D、E 在同一直线上,若 AE=15,DE=7,求 AB的长度.(3)探究发现:如图 3,P为等边△ ABC内一点,且∠APC=150° ,且∠ APD= 30° , AP=5,CP=4,DP=8,求BD的长.3、如图 1,△ ABC中, CD⊥AB于 D,且 BD:AD: CD=2:3:4,(1)试说明△ ABC是等腰三角形;(2)已知 S△ABC=10cm2,如图 2,动点 M从点 B 出发以每秒1cm的速度沿线段BA 向点 A 运动, 同时动点 N从点 A 出发以相同速度沿线段AC向点 C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t (秒),①若△ DMN的边与 BC平行,求t 的值;②若点 E 是边 AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.4、已知,△ ABC中,AC=BC,∠ACB=90° ,D为 AB 的中点,若 E 在直线 AC上任意一点,DF⊥DE,交直线 BC于 F 点. G为 EF 的中点,延长CG交 AB于点 H.(1)若 E 在边 AC上.①试说明DE=DF;②试说明CG=GH;(2)若 AE=3,CH=5.求边 AC的长.5、如图①,在矩形ABCD中, AB=5,AD=, AE⊥BD,垂足是 E. 点 F 是点 E 关于 AB的对称点,连结 AF,BF. (1) 求 AE和 BE的长.(2) 若将△ ABF沿着射线BD方向平移, 设平移的距离为m( 平移距离指点B 沿 BD方向所经过的线段长度 ) .当点 F分别平移到线段AB,AD上时,直接写出相应的m的值.(3) 如图②,将△ ABF绕点 B顺时针旋转一个角α (0 ° < α <180°) ,记旋转中的△ABF为△ A′BF′ ,在旋转过程中,设A′F′ 所在...