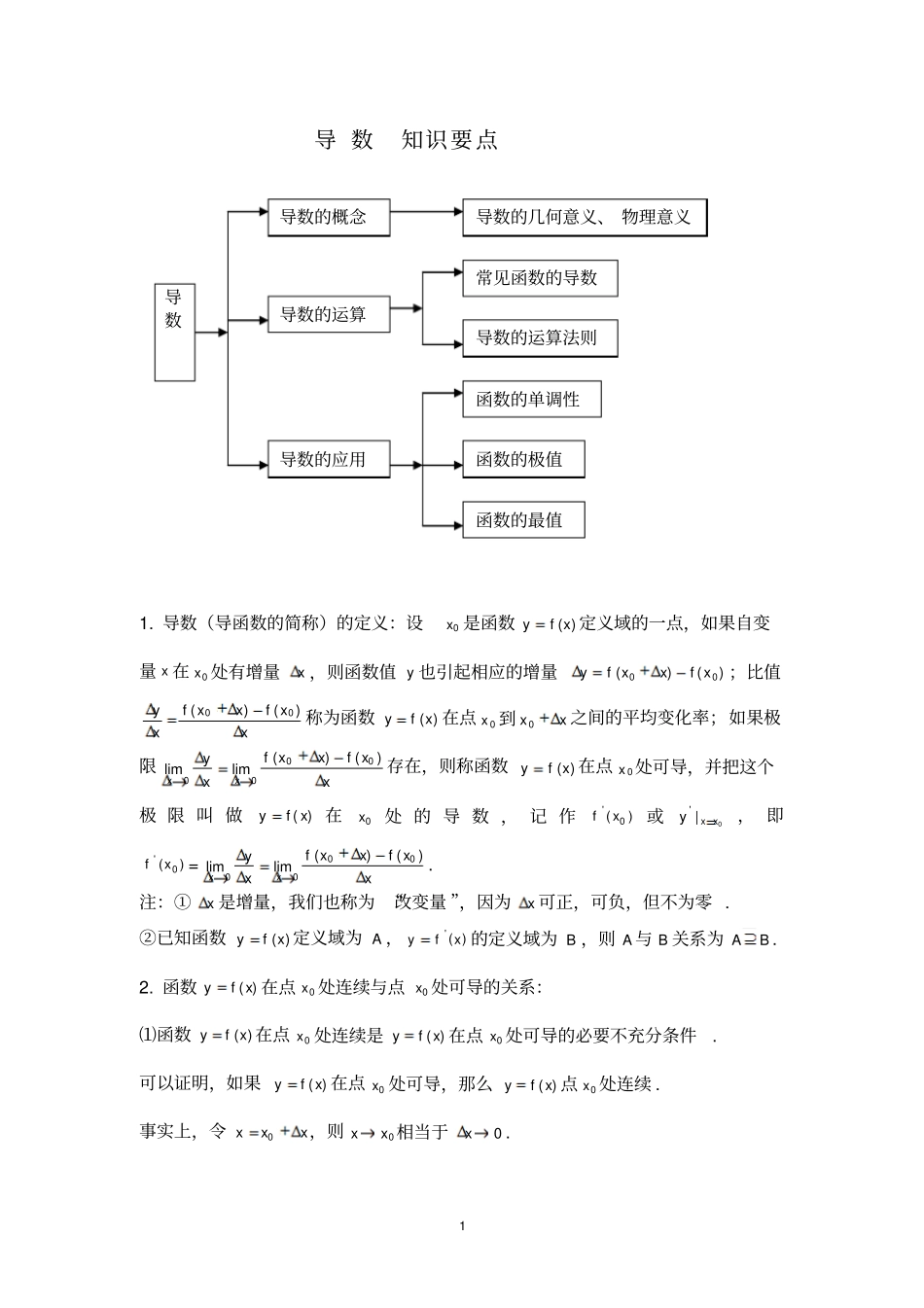
1 导 数知识要点1. 导数(导函数的简称)的定义:设0x 是函数)(xfy定义域的一点,如果自变量 x 在0x 处有增量x ,则函数值 y 也引起相应的增量)()(00xfxxfy;比值xxfxxfxy)()(00称为函数)(xfy在点0x 到xx 0之间的平均变化率;如果极限xxfxxfxyxx)()(limlim0000存在,则称函数)(xfy在点0x 处可导,并把这个极 限 叫 做)( xfy在0x处 的 导 数 , 记 作)(0' xf或0|'xxy, 即)(0' xf=xxfxxfxyxx)()(limlim0000. 注:①x 是增量,我们也称为 “改变量 ”,因为x 可正,可负,但不为零 . ②已知函数)(xfy定义域为 A ,)(' xfy的定义域为 B ,则 A 与 B 关系为BA. 2. 函数)(xfy在点0x 处连续与点0x 处可导的关系:⑴函数)(xfy在点0x 处连续是)(xfy在点0x 处可导的必要不充分条件. 可以证明,如果)(xfy在点0x 处可导,那么)(xfy点0x 处连续 . 事实上,令xxx0,则0xx相当于0x. 导数导数的概念导数的运算导数的应用导数的几何意义、 物理意义函数的单调性函数的极值函数的最值常见函数的导数导数的运算法则2 于是)]()()([lim)(lim)(lim0000000xfxfxxfxxfxfxxxx).()(0)()(limlim)()(lim)]()()([lim000'0000000000xfxfxfxfxxfxxfxfxxxfxxfxxxx⑵如果)(xfy点0x 处连续,那么)(xfy在点0x 处可导,是不成立的 . 例:||)(xxf在点00x处连续,但在点00x处不可导,因为xxxy||,当x >0 时,1xy;当x <0 时,1xy,故xyx0lim不存在 . 注:①可导的奇函数函数其导函数为偶函数. ②可导的偶函数函数其导函数为奇函数. 3. 导数的几何意义:函数)(xfy在点0x 处的导数的几何意义就是曲线)(xfy在点))(,(0xfx处的切线的斜率,也就是说,曲线)(xfy在点 P))(,(0xfx处的切线的斜率是)(0' xf,切线方程为).)((0'0xxxfyy4、几种常见的函数导数:0'C( C 为常数)1')(nnnxx(Rn)xxc o s)( s i n 'xxs i n)( c o s'xx1)(ln'exxaal o g1)( l o g'xxee')(aaaxxln)('5. 求导数的四则运算法则:''')(vuvu)(...)()()(...)()(''2'1'21xfxfxfyxfxfxfynn''''''')()(cvcvvccvuvvuuv( c 为常数))0(2'''vvuvvuvu注:①vu, 必须是可导函数 . ②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导. 例如:设xxxf2sin2)(,xxxg2cos)(,则)(),(xgxf在0x处均不可导,但它们和)()(xgxfxxcossin在0x处均可导 . 3 6. 复合函数的求导法则:)...