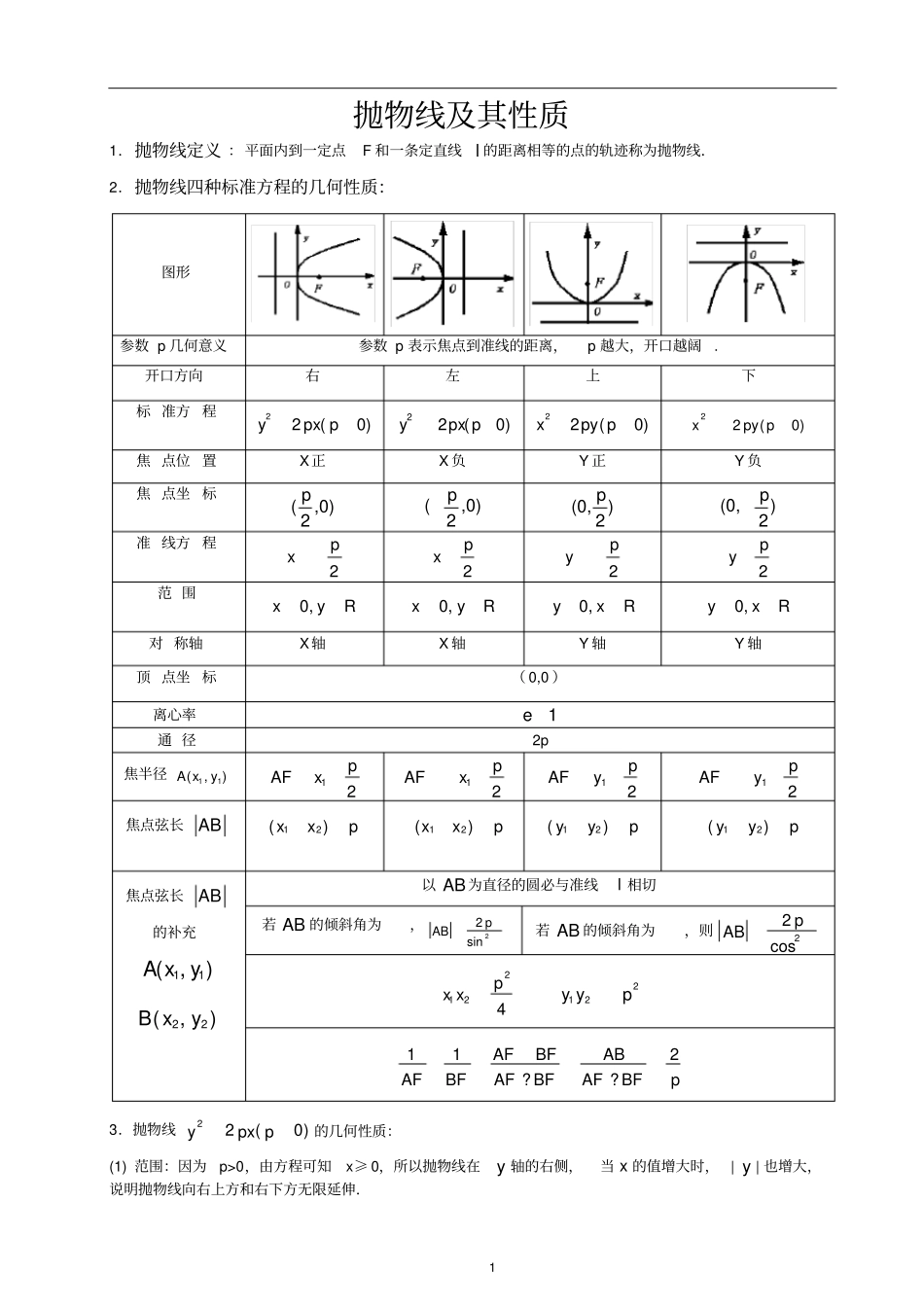
1 抛物线及其性质1.抛物线定义 :平面内到一定点F 和一条定直线 l 的距离相等的点的轨迹称为抛物线.2.抛物线四种标准方程的几何性质:图形参数 p 几何意义参数 p 表示焦点到准线的距离,p 越大,开口越阔. 开口方向右左上下标 准方 程22(0)ypx p22(0)ypx p22(0)xpy p22(0)xpy p焦 点位 置X正X 负Y 正Y 负焦 点坐 标(,0)2p(,0)2p(0,)2p(0,)2p准 线方 程2px2px2py2py范 围0,xyR0,xyR0,yxR0,yxR对 称轴X轴X 轴Y 轴Y 轴顶 点坐 标( 0,0 )离心率1e通 径2p 焦半径11(,)A xy12pAFx12pAFx12pAFy12pAFy焦点弦长AB12()xxp12()xxp12()yyp12()yyp焦点弦长AB的补充11(,)A x y22(,)B xy以 AB为直径的圆必与准线l 相切若 AB 的倾斜角为,22sinpAB若 AB 的倾斜角为,则22cospAB2124px x212y yp112AFBFABAFBFAFBFAFBFp??3.抛物线)0(22ppxy的几何性质:(1) 范围:因为p>0,由方程可知x≥ 0,所以抛物线在y 轴的右侧,当 x 的值增大时, | y | 也增大,说明抛物线向右上方和右下方无限延伸.2 (2) 对称性:对称轴要看一次项,符号决定开口方向.(3) 顶点( 0,0),离心率:1e,焦点(,0)2pF,准线2px,焦准距 p.(4) 焦点弦:抛物线)0(22ppxy的焦点弦 AB ,),(11 yxA,),(22 yxB, 则pxxAB21||.弦长 |AB|=x1+x2+p, 当 x 1=x2 时,通径最短为2p。4.焦点弦的相关性质:焦点弦 AB ,),(11 yxA,),(22 yxB,焦点(,0)2pF(1) 若 AB 是抛物线22(0)ypx p的焦点弦(过焦点的弦),且11( ,)A x y,22(,)B xy,则:21 24pxx,21 2yyp 。(2) 若 AB是抛物线22(0)ypx p的焦点弦,且直线AB的倾斜角为α ,则22sinPAB(α ≠ 0)。(3) 已知直线 AB是过抛物线22(0)ypx p焦点 F ,112AFBFABAFBFAFBFAFBFp??(4) 焦点弦中通径最短长为2p。通径:过焦点垂直于焦点所在的轴的焦点弦叫做通径.(5) 两个相切:○1 以抛物线焦点弦为直径的圆与准线相切. ○2 过抛物线焦点弦的两端点向准线作垂线,以两垂足为直径端点的圆与焦点弦相切。5.弦长公式:),(11 yxA,),(22 yxB是抛物线上两点,则221212()()ABxxyy||11||1212212yykxxk6. 直线与抛物线的位置关系直线,抛物线,,消 y 得:(1)当 k=0 时,直线 l 与抛物线的对称轴平行,有一个交点;(2)当 k≠0 时,Δ > 0,直线 l 与抛物线相交,两个不同交点;Δ =0, 直线 l 与抛物线相切,一个切点;Δ < ...