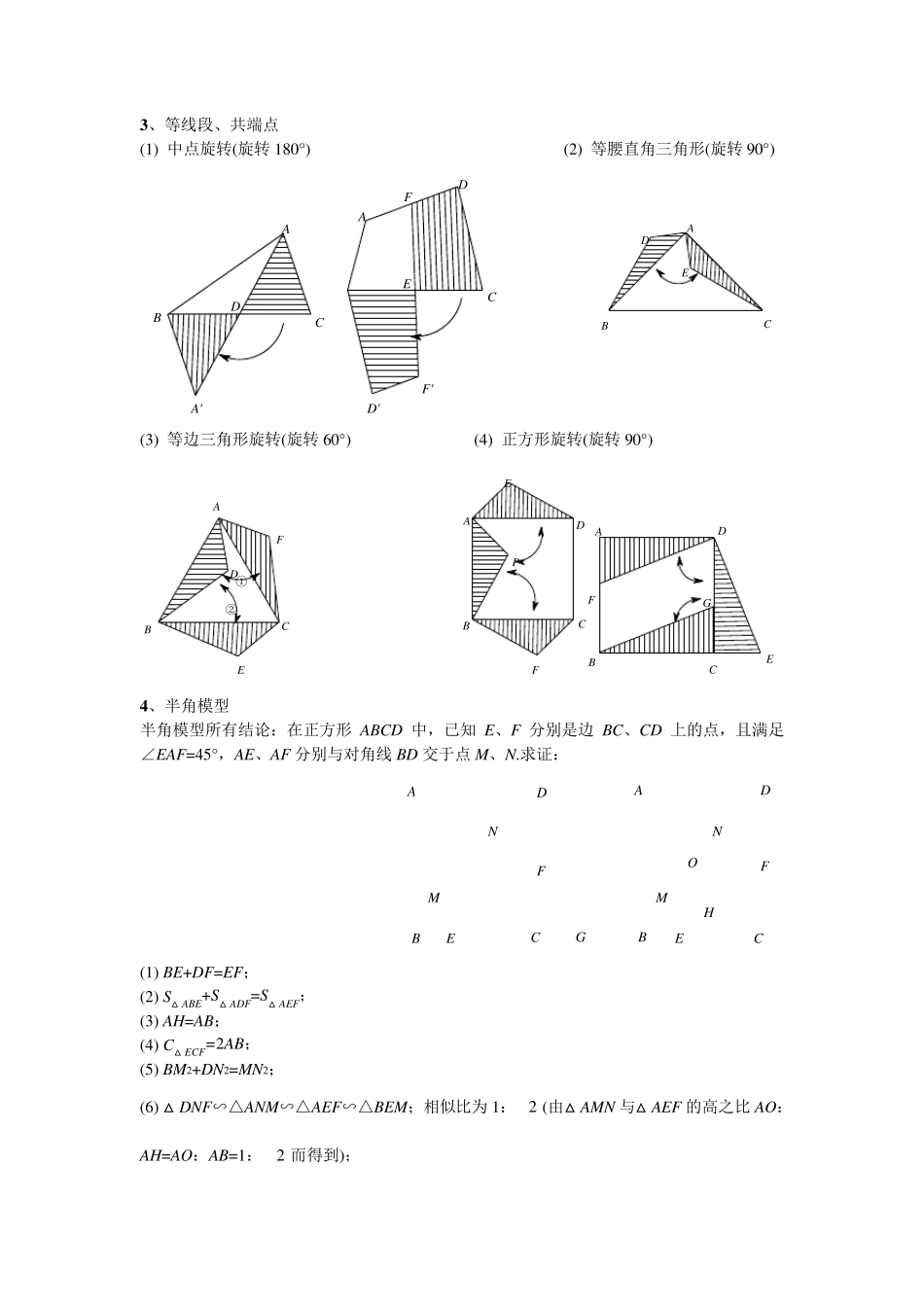
如何短时间突破数学压轴题 还有不到一个月的时间就要进行期中考试了,期中考试的重要性不必多说。各区期中考试的范围相信学生们都已经非常清楚。 个人觉得现在大部分学生的困难在于旋转、圆,由于时间比较紧张,给大家一些复习资料和学习方法,希望能够帮到大家。 一、旋转: 纵观几年的数学试卷,最难的几何题几乎都是旋转,在此给出旋转中最常见的几何模型和一些解题技巧。 旋转模型: 1 、三垂直全等模型 三垂直全等构造方法:从等腰直角三角形的两个锐角顶点出发向过直角顶点的直线作垂线。 EDCABEDCAB 2 、手拉手全等模型 手拉手全等基本构图: CCCABDEABDEEDBAEDCBAEDCBA ABCDEEDCBA EDCBA3 、等线段、共端点 (1) 中点旋转(旋转180°) (2) 等腰直角三角形(旋转90°) A'DCBAF'D'FEDCA (3) 等边三角形旋转(旋转60°) (4) 正方形旋转(旋转90°) ②①FEDCBA PFEDCBAGFEDCBA 4 、半角模型 半角模型所有结论:在正方形ABCD 中,已知E、F 分别是边BC、CD 上的点,且满足∠EAF=45°,AE、AF 分别与对角线BD 交于点M、N.求证: NMFEDCBAGOAHNMFEDCB (1) BE+DF=EF; (2) S△ABE+S△ADF=S△AEF; (3) AH=AB; (4) C△ECF=2AB; (5) BM2+DN2=MN2; (6) △DNF∽△ANM∽△AEF∽△BEM;相似比为 1:2 (由△AMN 与△AEF 的高之比 AO: AH=AO:AB=1:2 而得到); MEDCBA(7) S△AMN=S四边形MNFE; (8) △AOM∽△ADF,△AON∽△ABE; (9) ∠AEN 为等腰直角三角形,∠AEN=45°.(1. ∠EAF=45°;2.AE:AN=1:2 ) 解题技巧: 1.遇中点,旋180°,构造中心对称 例:如图,在等腰ABC△中,ABAC,ABC,在四边形BDEC 中,DBDE,2BDE,M 为CE 的中点,连接 AM ,DM . ⑴ 在图中画出DEM△关于点M 成中心对称的图形; ⑵ 求证:AMDM; ⑶ 当 ___________时,AMDM. [解析]⑴ 如图所示; ⑵ 在⑴的基础上,连接ADAF, 由⑴中的中心对称可知,DEMFCM△≌△, ∴ DEFCBD,DMFM,DEMFCM , 360ABDABCCBDBDEDEMBCE 360DEMBCE, 360360ACFACEFCMBCEFCM, ∴ABDACF , ∴ABDACF△≌△,∴ ADAF, DMFM,∴ AMDM. ⑶ 45 . 2.遇90°。旋90°,造垂直; 例:请阅读下列材料: 已知:如图 1 在 Rt ABC中,90B...