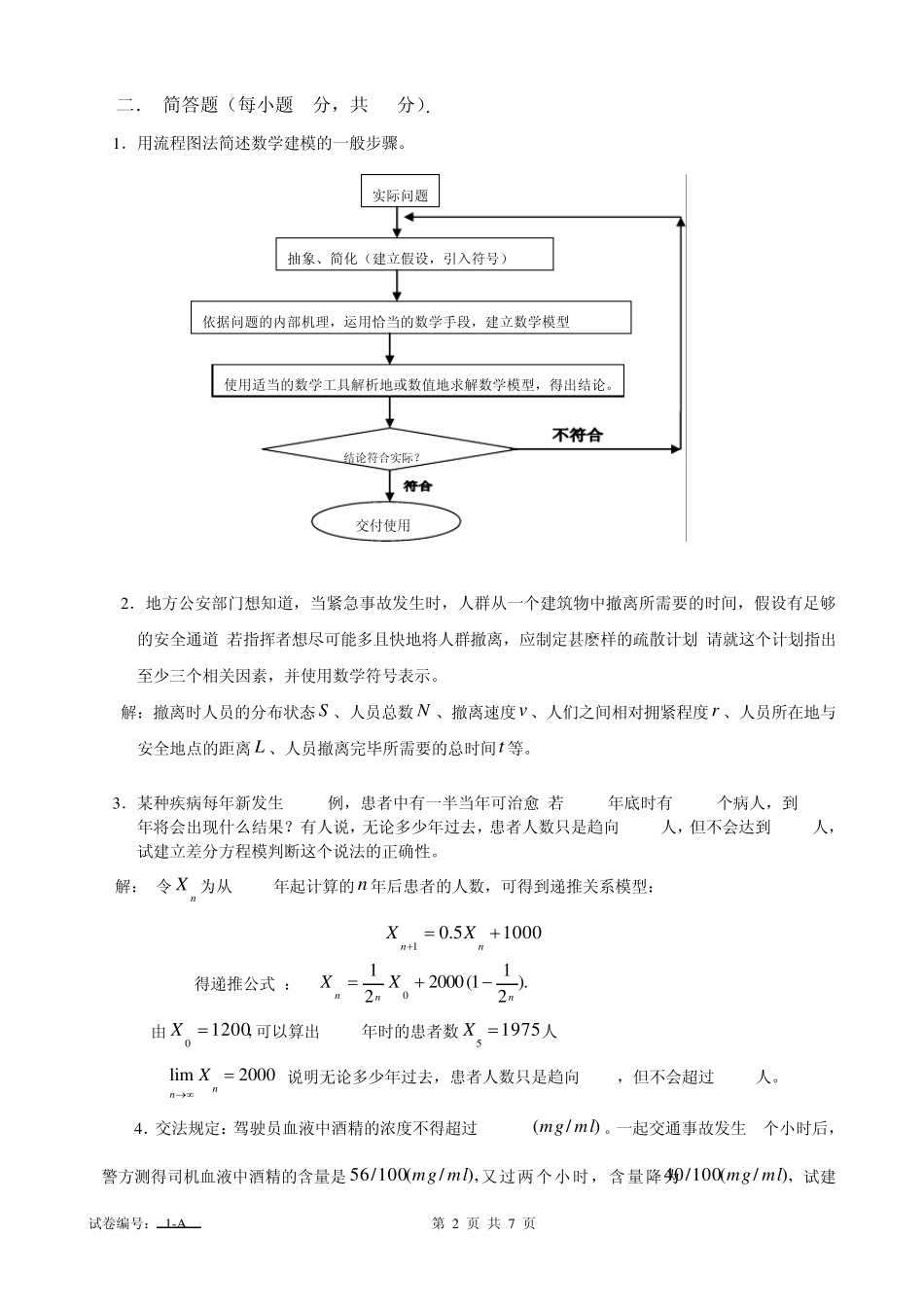
试卷编号: 1-A 第 1 页 共 7 页 天津理工大学考试试卷 2008~ 2009 学年度第二学期 《数学模型》 期末考试试卷 评分参考标准 课程代码: 1502011 试卷编号: 1-A 命题日期: 2009 年 5 月 26 日 答题时限: 120 分钟 考试形式:开卷、笔试+机试 一. 填空题(每小题5分,共15分). 1.设某种物资有两个产地21, AA,其产量分别为 10、20,两个销地21,BB的销量相等均为 15。 如果从任意产地到任意销地的单位运价都为 1。设ijx表示产地i 运往销地 j 的运量,则求最优运输方案的数学模型为: 15 15 20 10 .22122111222112112121xxxxxxxxstxMaxijij 2.设某区域开始时的人口数为0x ,时刻t 的人口数为)(tx,若区域允许的最大人口数为mx,人口增长率r 为,则该区域人口增长问题的逻辑斯蒂克模型为 0d( 1) ,( 0 ).dmxxrxxxtx 3. 一个刚获得学位的大学毕业生,在择业问题上,通常会从以下几个方面来考虑:收入丰厚;适合个人兴趣;发展前景广阔;地理位置优越。若有三个就业岗位可选,建立该择业问题的 AHP 模型为: 试卷编号: 1-A 第 2 页 共 7 页 二. 简答题(每小题5分,共20分). 1.用流程图法简述数学建模的一般步骤。 2.地方公安部门想知道,当紧急事故发生时,人群从一个建筑物中撤离所需要的时间,假设有足够的安全通道.若指挥者想尽可能多且快地将人群撤离,应制定甚麽样的疏散计划.请就这个计划指出至少三个相关因素,并使用数学符号表示。 解:撤离时人员的分布状态S 、人员总数N 、撤离速度v 、人们之间相对拥紧程度r 、人员所在地与安全地点的距离L 、人员撤离完毕所需要的总时间t 等。 3.某种疾病每年新发生1000例,患者中有一半当年可治愈.若2008年底时有1200个病人,到 2013年将会出现什么结果?有人说,无论多少年过去,患者人数只是趋向 2000人,但不会达到 2000人,试建立差分方程模判断这个说法的正确性。 解: 令nX 为从2008年起计算的n 年后患者的人数,可得到递推关系模型: 10005.01nnXX 得递推公式 : ).211(2000210nnnXX 由,12000 X可以算出2010年时的患者数19755 X人. L=lim2000nnX,说明无论多少年过去,患者人数只是趋向 2000,但不会超过 2000人。 4.交法规定:驾驶员血液中酒精的浓度不得超过 80/100 )/(mlmg。一起交通事故发生3个小时后,警方测得司...