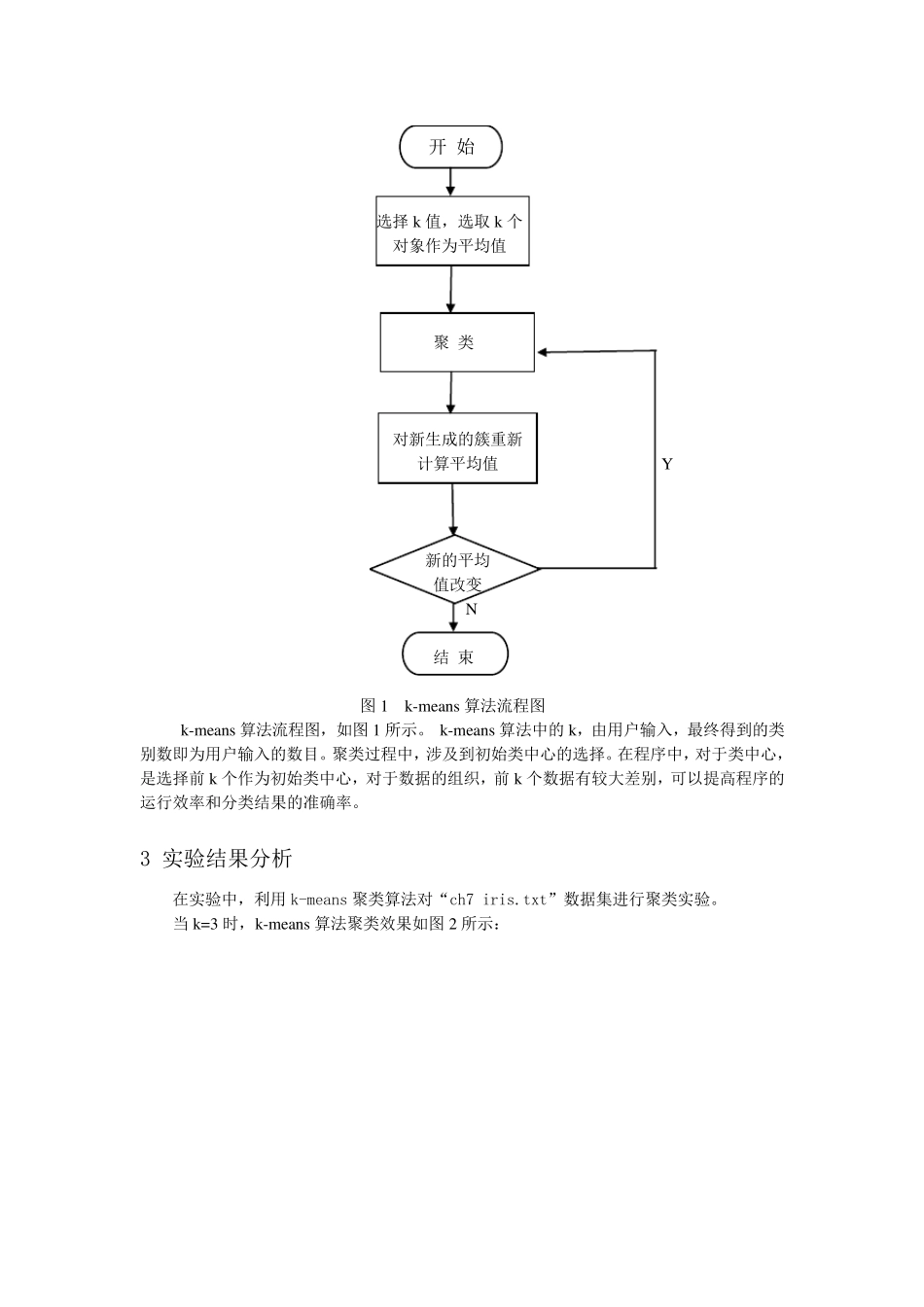
实验题目: 数据聚类实验 1 实验目的 (1)了解常用聚类算法及其优缺点; (2)掌握k-means 聚类算法对数据进行聚类分析的基本原理和划分方法。 (3)利用k-means 聚类算法对“ch7 iris.txt”数据集进行聚类实验。 (4)熟悉使用matlab 进行算法的实现。 2 实验步骤 2.1 算法原理 聚类就是按照某个特定标准(如距离准则)把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。即聚类后同一类的数据尽可能聚集到一起,不同数据尽量分离。 k-means 是划分方法中较经典的聚类算法之一。由于该算法的效率高,所以在对大规模数据进行聚类时被广泛应用。目前,许多算法均围绕着该算法进行扩展和改进。 k-means 算法以 k 为参数,把 n 个对象分成 k 个簇,使簇内具有较高的相似度,而簇间的相似度较低。k-means 算法的处理过程如下:首先,随机地 选择k 个对象,每个对象初始地代表了一个簇的平均值或中心;对剩余的每个对象,根据其与各簇中心的距离,将它赋给最近的簇;然后重 新 计 算每个簇的平均值。 这 个过程不断 重 复 ,直 到准则函 数收 敛 。 通 常,采 用平方误 差准则,其定义 如下: kiCpiimpE12 ,这 里 E 是数据集中所有对象的平方误 差的总 和,p 是空 间中的点,im 是簇iC 的平均值。该目标函 数使生 成的簇尽可能紧 凑 独 立 ,使用的距离度量是欧 几 里 得距离,当 然也可以用其他 距离度量。 本实验便 采 用k-means 聚类方法对样 本数据对象进行聚类。该方法易 实现,对不存 在极大值的数据有很 好 的聚类效果 ,并 且 对大数据集有很 好 的伸 缩 性。 2.2 算法流 程 本实验采 用的是 k-means 聚类算法,类中心的选择基于簇中对象的平均值。 (1)获 取 用户 的类中心数目k 和具有 n 个对象的数据集; (2)任 意 选取 k 个对象作 为初始的簇中心; (3)根据簇中对象的平均值,将每个对象重 新 赋给最类似的簇; (4)更 新 簇的平均值,即类中心,重 新 计 算每个簇中对象的平均值; (5)如果 新 的平均值发 生 改变 ,转 至 (2)步; (6)新 的平均值不在发 生 改变 ,算法聚类结 束 。 2.2 算法流 程图 开 始 选择k 值,选取k 个 对象作为平均值 聚 类 对新生成的簇重新 计算平均值 Y ...