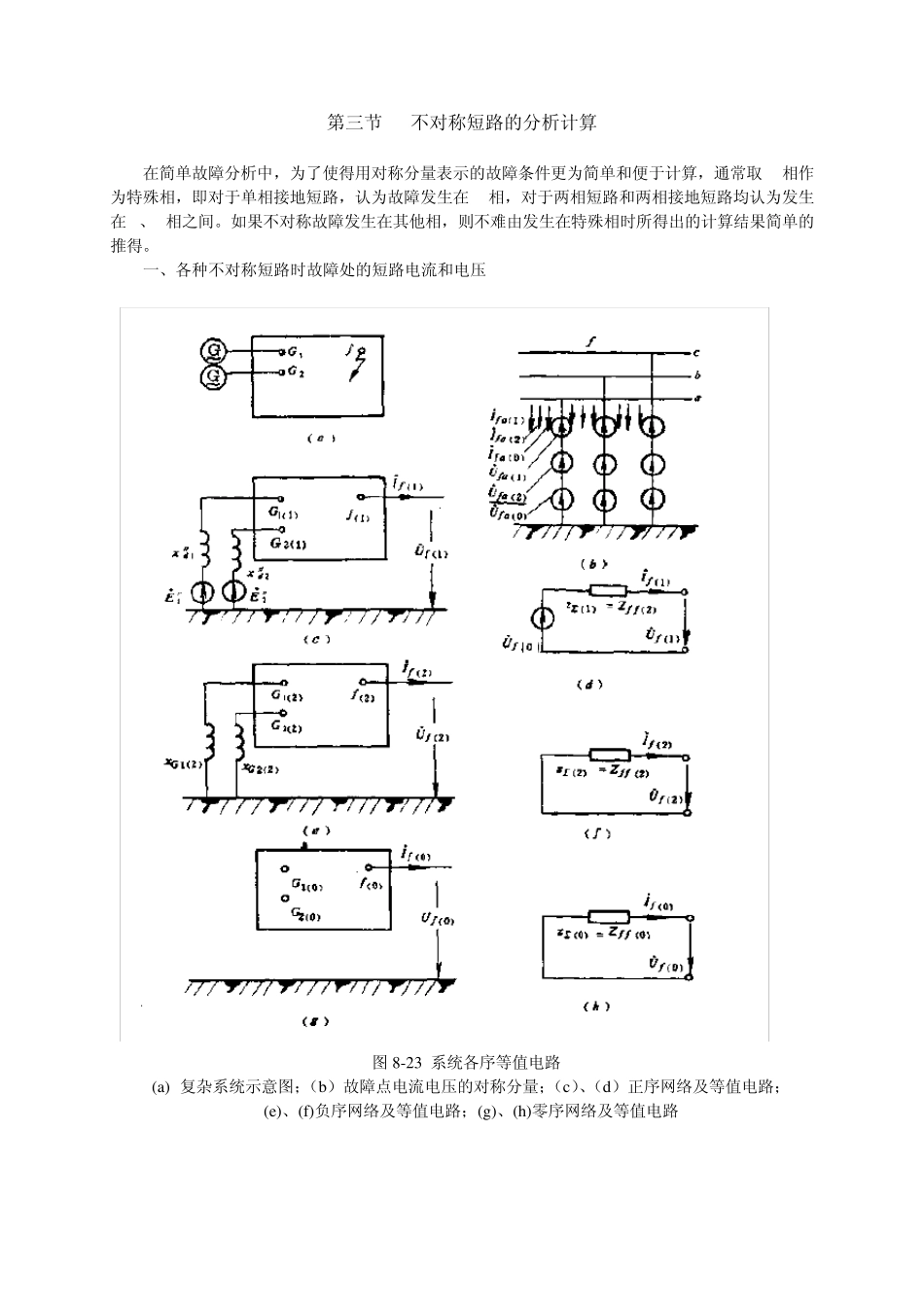
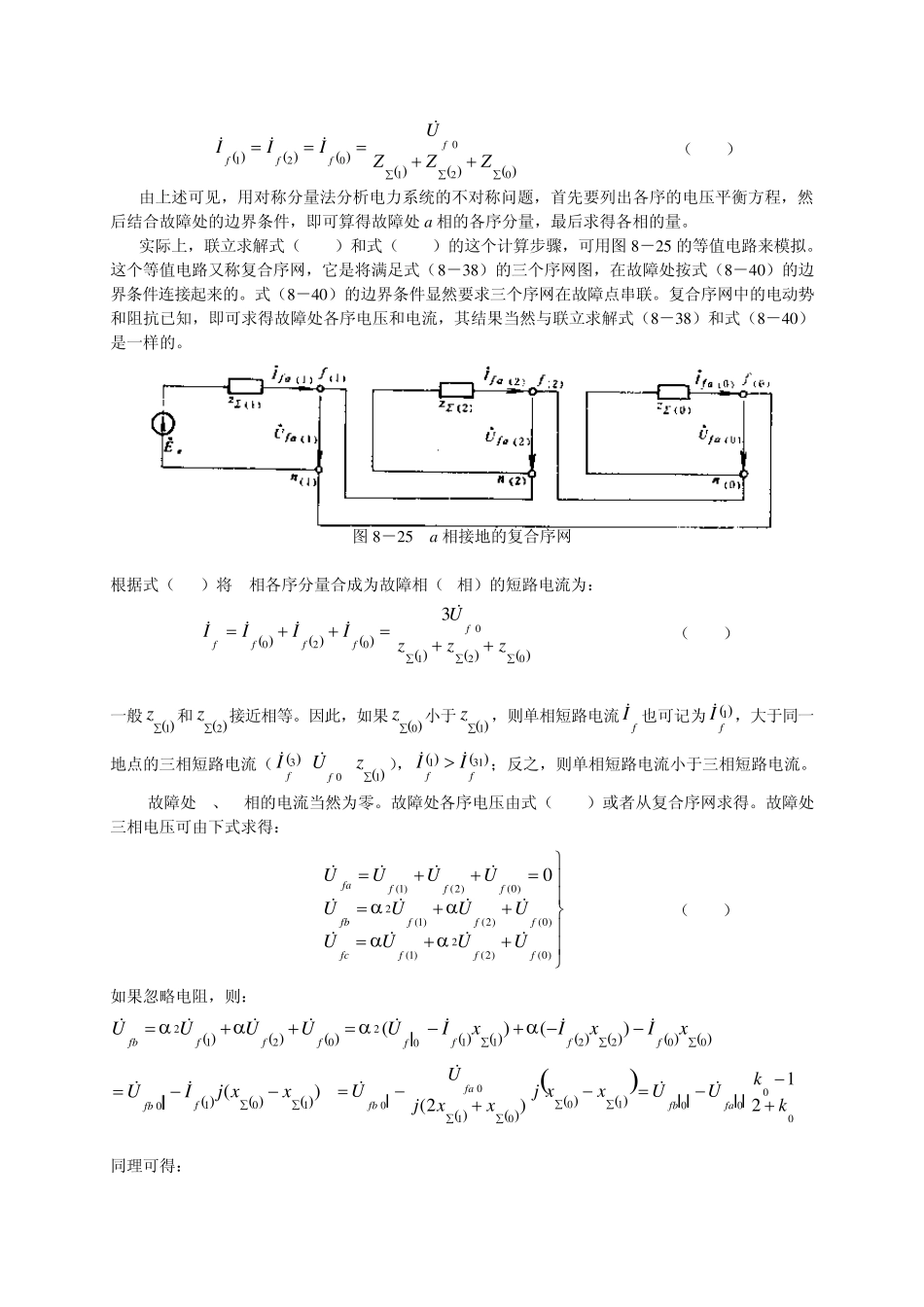
第三节 不对称短路的分析计算 在简单故障分析中,为了使得用对称分量表示的故障条件更为简单和便于计算,通常取a相作为特殊相,即对于单相接地短路,认为故障发生在a相,对于两相短路和两相接地短路均认为发生在b、c相之间。如果不对称故障发生在其他相,则不难由发生在特殊相时所得出的计算结果简单的推得。 一、各种不对称短路时故障处的短路电流和电压 图 8-23 系统各序等值电路 (a) 复杂系统示意图;(b)故障点电流电压的对称分量;(c)、(d)正序网络及等值电路; (e)、(f)负序网络及等值电路;(g )、(h )零序网络及等值电路 图8-23(a)表示一个任意复杂的电力系统,1G 、2G 代表发电机端点,在 f点发生不对称短路后,f 点的三相对地电压faU、fbU、fcU和由 f 点流出的三相电流(即短路电流)faI、fbI、fcI均为三相不对称,而这时发电机的电动势仍为三相对称的正序电动势,各元件的三相参数也对称。如果将故障处电压和短路电流分解成三组对称分量,如图8-23(b)所示,则根据第一节对三相对称元件序分量的独立性的分析,发电机、变压器和线路上各序电压只与各序电流有关。根据叠加原理,将图8-23(b)分解为正序、负序和零序三个序网,如图8-23(c)、(e)、(g)。利用戴维南定理将正序、负序和零序三个序网化简为对应的正序、负序和零序等值电路,如图8-23(d)、(f)、(h),正序网络中节点 1f的自阻抗 1ffZ即为从 1f点看进网络的等值阻抗 1Z。0fU为 1f点正常时电压,即开路电压。负序网络中发电机的负序电抗2Gx可近似等于dx 。同样, 22ffZz。零序网络结构和正序网络是不相同的。由于发电机中性点往往是不接地的,其零序阻抗开路。同样, 00ffZz。由于各序本身对称,根据三个序网的等值电路,可以写出 a 相的电压平衡关系: 101122200000fffffffUUIzUIzUIz (8-38) 式中省略了下标 a。在分析简单故障时,一般总以 a相为参考相,故在以后的分析中,表示a相序分量时均省略了下标 a。在式(8 -3 8 )中有六个未知数(故障点的三序电压和三序电流),但方程只有三个,故还不能求解故障处的各序电压和电流。这是很明显的,因为式(8 -3 8 )没有反映故障处的不对称性质,而只是一般地列出了各序分量的电压平衡关系。...