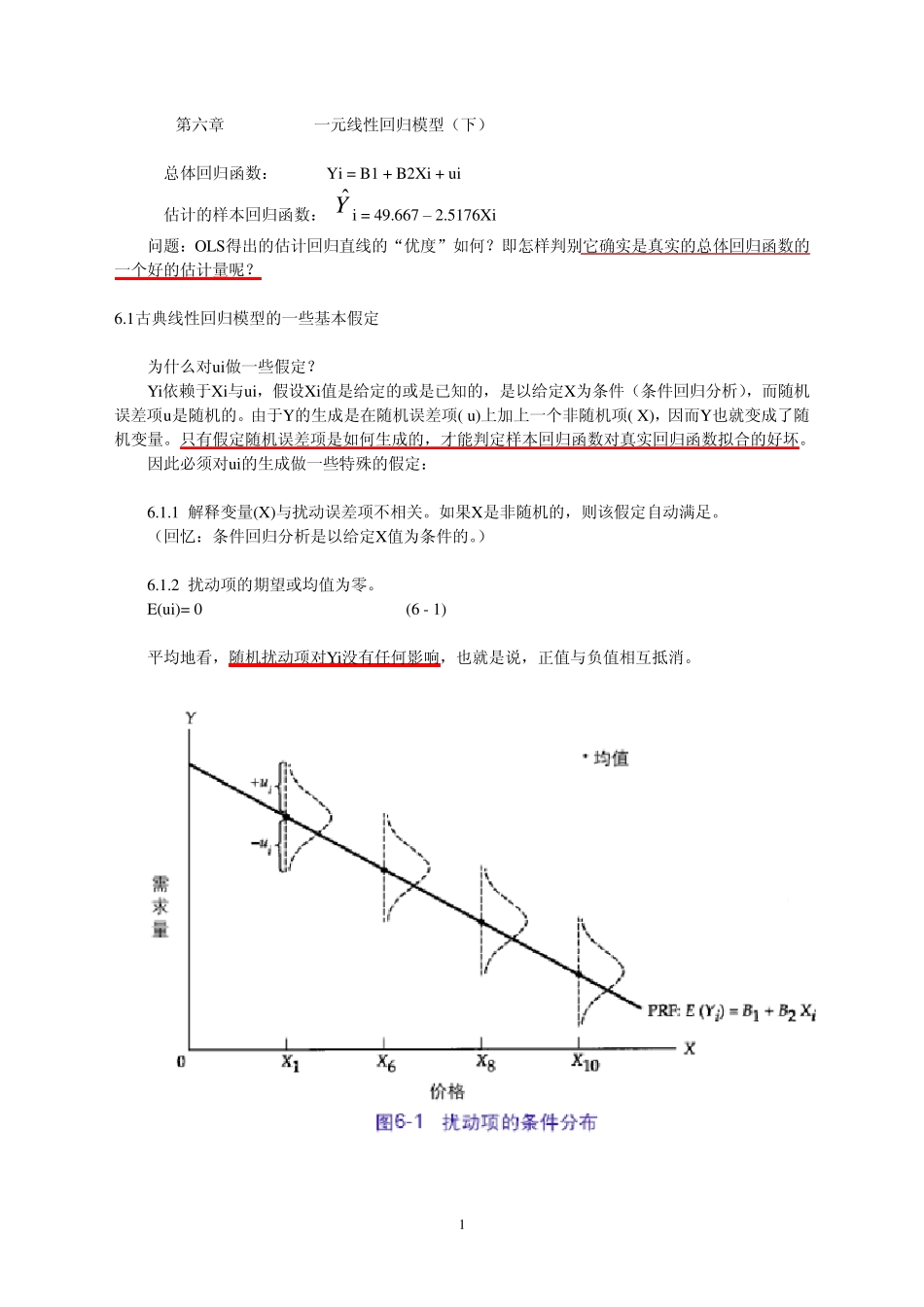
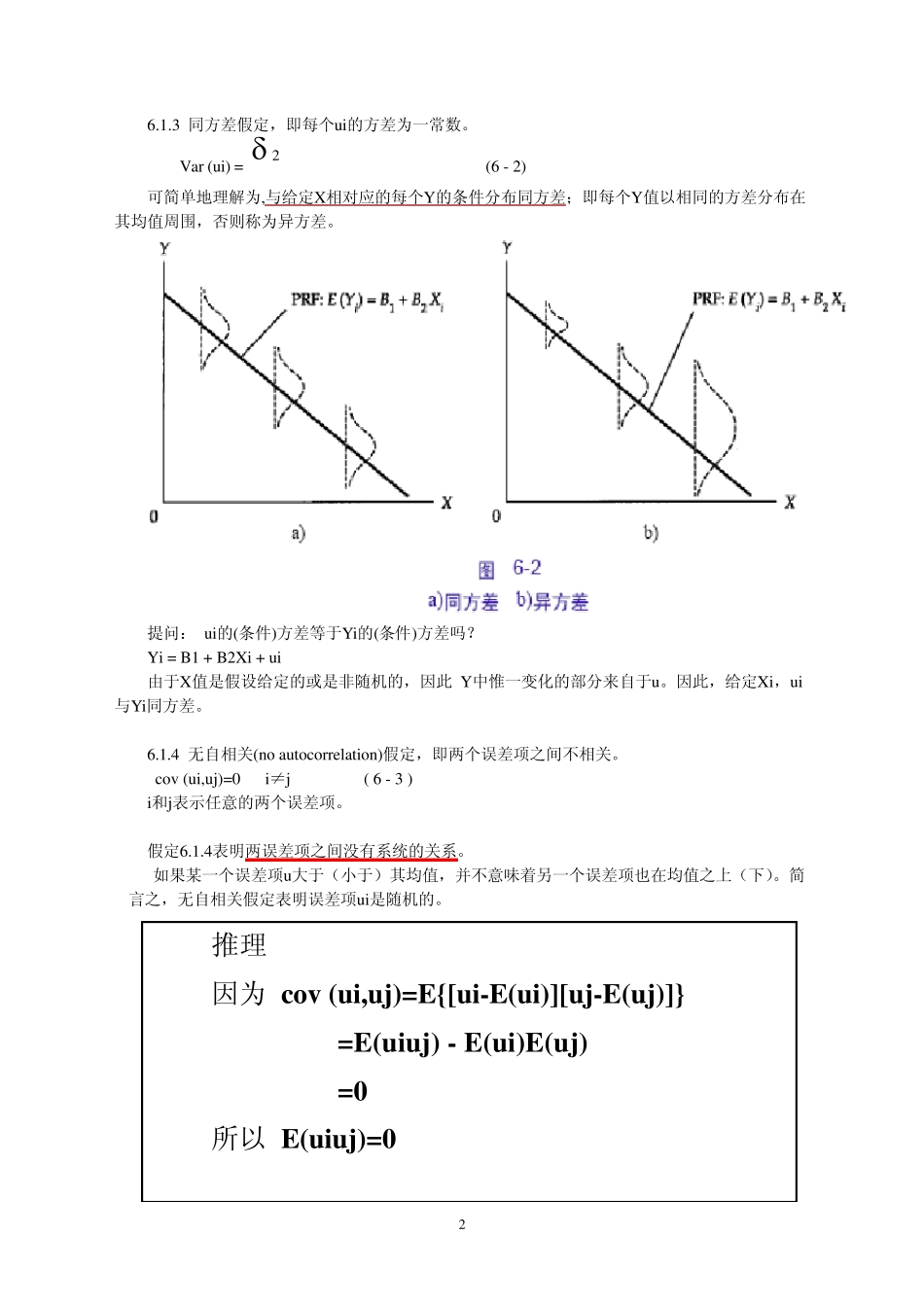
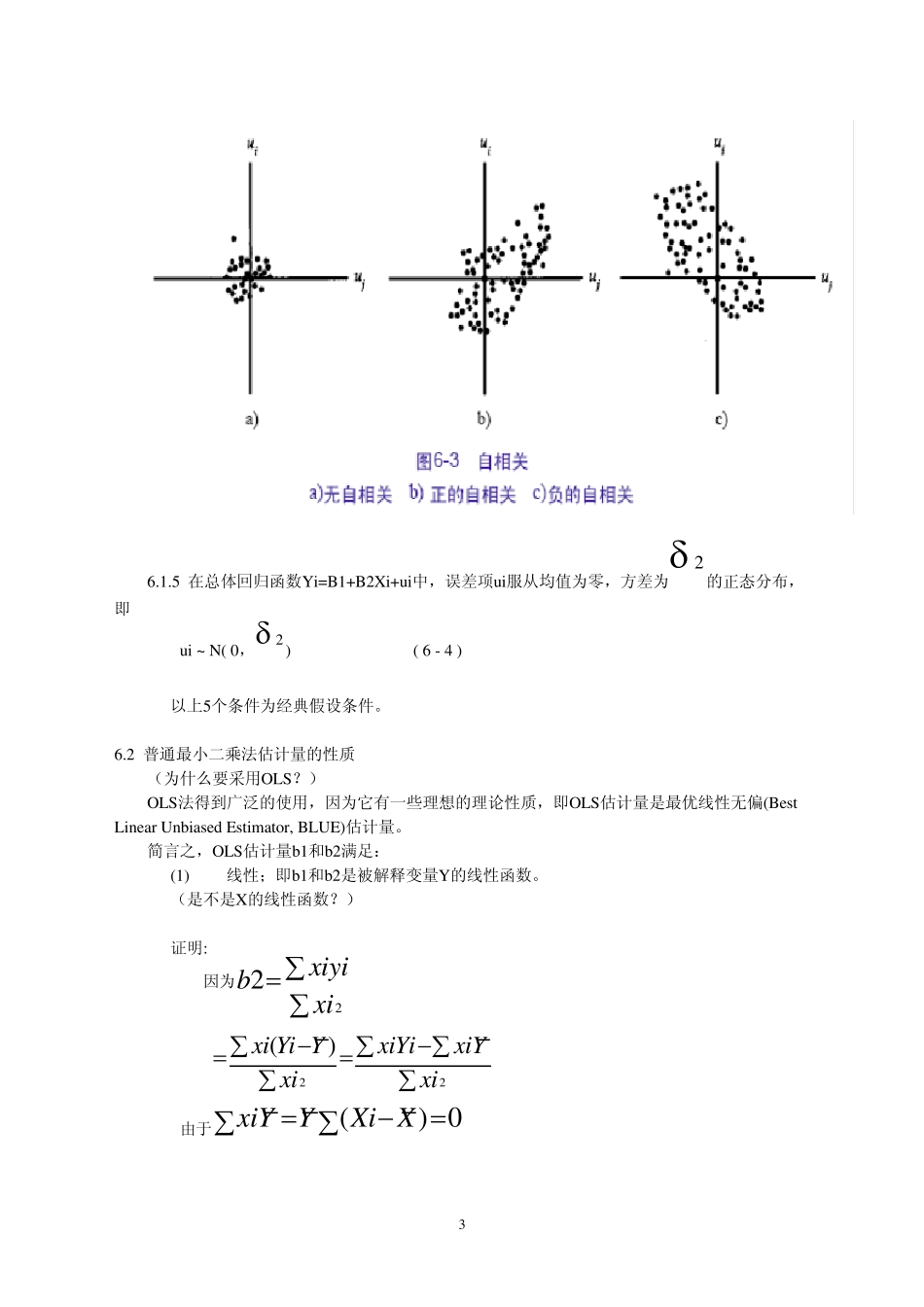
1 第六章 一元线性回归模型(下) 总体回归函数: Yi = B1 + B2Xi + u i 估计的样本回归函数: ˆY i = 49.667 – 2.5176Xi 问题:OLS得出的估计回归直线的“优度”如何?即怎样判别它确实是真实的总体回归函数的一个好的估计量呢? 6.1古典线性回归模型的一些基本假定 为什么对u i做一些假定? Yi依赖于Xi与u i,假设Xi值是给定的或是已知的,是以给定X为条件(条件回归分析),而随机误差项u 是随机的。由于Y的生成是在随机误差项( u )上加上一个非随机项( X),因而Y也就变成了随机变量。只有假定随机误差项是如何生成的,才能判定样本回归函数对真实回归函数拟合的好坏。 因此必须对u i的生成做一些特殊的假定: 6.1.1 解释变量(X)与扰动误差项不相关。如果X是非随机的,则该假定自动满足。 (回忆:条件回归分析是以给定X值为条件的。) 6.1.2 扰动项的期望或均值为零。 E(u i)= 0 (6 - 1) 平均地看,随机扰动项对Yi没有任何影响,也就是说,正值与负值相互抵消。 2 6.1.3 同方差假定,即每个u i的方差为一常数。 Var (u i) = 2 (6 - 2) 可简单地理解为,与给定X相对应的每个Y的条件分布同方差;即每个Y值以相同的方差分布在其均值周围,否则称为异方差。 提问: u i的(条件)方差等于Yi的(条件)方差吗? Yi = B1 + B2Xi + u i 由于X值是假设给定的或是非随机的,因此 Y中惟一变化的部分来自于u 。因此,给定Xi,u i与Yi同方差。 6.1.4 无自相关(no au tocorrelation)假定,即两个误差项之间不相关。 cov (u i,u j)=0 i≠j ( 6 - 3 ) i和j表示任意的两个误差项。 假定6.1.4表明两误差项之间没有系统的关系。 如果某一个误差项u 大于(小于)其均值,并不意味着另一个误差项也在均值之上(下)。简言之,无自相关假定表明误差项u i是随机的。推理 因为 cov (ui,uj)=E{[ui-E(ui)][uj-E(uj)]} =E(uiuj) - E(ui)E(uj) =0 所以 E(uiuj)=0 3 6.1.5 在总体回归函数Yi=B1+B2Xi+ui中,误差项ui服从均值为零,方差为2的正态分布,即 ui ~ N( 0,2) ( 6 - 4 ) 以上5个条件为经典假设条件。 6.2 普通最小二乘法估计量的性质 (为什么要采用OLS?) OLS法得到广泛的使用,因为它有一些理想的理论性质,即OLS估计量是最优线性无偏(Best Linear Unbiased Estimator, BLUE)估计量。 简言之,OLS估计量b1和b2满足: (1) 线性;...