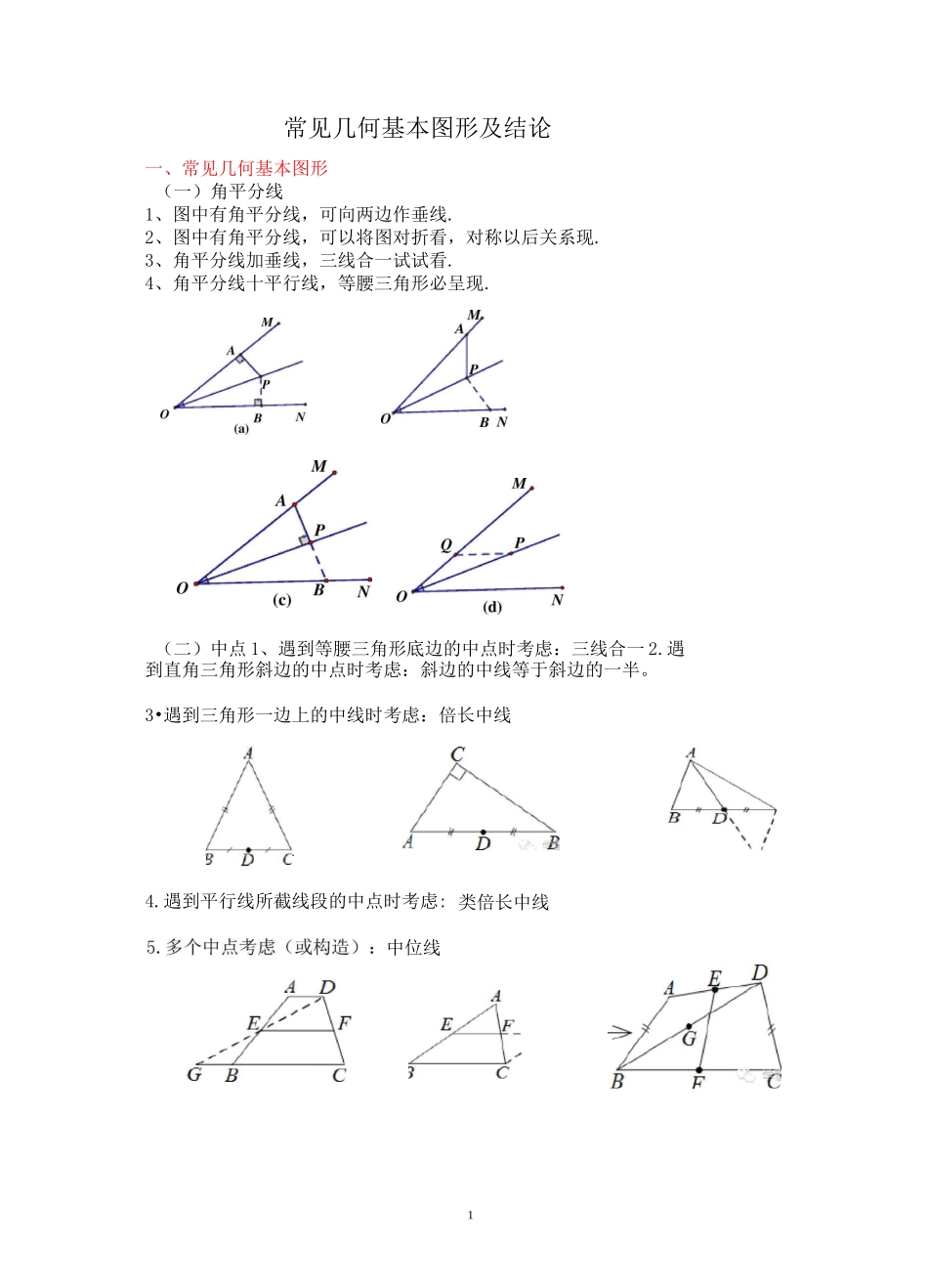
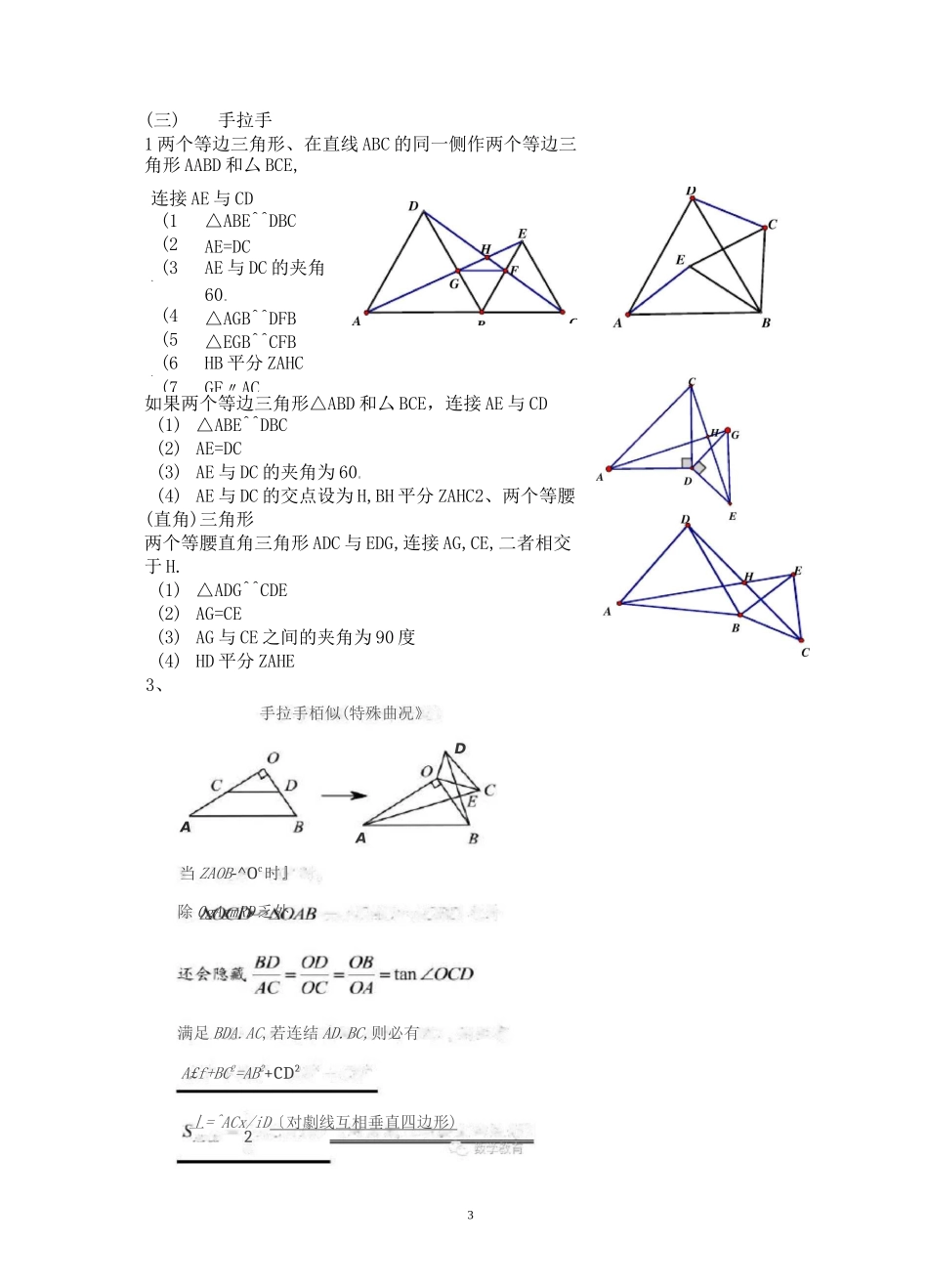
1常见几何基本图形及结论一、常见几何基本图形(一)角平分线1、图中有角平分线,可向两边作垂线.2、图中有角平分线,可以将图对折看,对称以后关系现.3、角平分线加垂线,三线合一试试看.4、角平分线十平行线,等腰三角形必呈现.(二)中点 1、遇到等腰三角形底边的中点时考虑:三线合一 2.遇到直角三角形斜边的中点时考虑:斜边的中线等于斜边的一半。3•遇到三角形一边上的中线时考虑:倍长中线4.遇到平行线所截线段的中点时考虑: 类倍长中线中位线6.MAEEC1D小蚌饰'百信长中线类模型③AMDM;④CE±AD辅册线:有平 4rAB//CDT有中 AAM=DM延 EMt构造 X 倔 SAD 则‘连接 CM 枸i 圭等腰 AZF.WC,AMC77逮过枸 it 呂 宇奎等线段数量及位置关系,角的大 :① 平苻四边形;ABCD②EC"AB;结:ZEMD=^ZMEA7FrBBAE相似三形 360 度谨转模型(倍长屮线法〉②EF^CF结论:① DF=RF:②DF 丄 EF辅助线 : 延长 DF 到点 GT使 FG=DFT主無 CG、RG、BD 证明 ABDG 为等腰直帘究占杞点:A.4BD^ACBG条件:① A.4DE.^4BC 均为等腰直角堆点:证明 ZBAD=ZBCG2连接 AE 与 CD(1)△ABE^^DBC(2)AE=DC(3)AE 与 DC 的夹角60。(4)△AGB^^DFB(5)△EGB^^CFB(6)HB 平分 ZAHC(7GF〃AC3(三)手拉手1 两个等边三角形、在直线 ABC 的同一侧作两个等边三角形 AABD 和厶 BCE,如果两个等边三角形△ABD 和厶 BCE,连接 AE 与 CD(1) △ABE^^DBC(2) AE=DC(3) AE 与 DC 的夹角为 60。(4) AE 与 DC 的交点设为 H,BH 平分 ZAHC2、两个等腰(直角)三角形两个等腰直角三角形 ADC 与 EDG,连接 AG,CE,二者相交于 H.(1) △ADG^^CDE(2) AG=CE(3) AG 与 CE 之间的夹角为 90 度(4) HD 平分 ZAHEC3、DAA丄=^ACx/iD〔对劇线互相垂直四边形 ) 2手拉手栢似(特殊曲况》当 ZAOB-^Oc时』除 0gAgmRD 乏外满足 BDA.AC,若连结 AD.BC,则必有A£f+BC2=AB2+CD2OD+OE=OCOC 平分 ZAOB,D、E 在 OA、OB 上已知:ZAOB=120。,ZDCE=60。,4(四).对角互补1、全等型—90°ZAOB=ZDCE=90。,OC 平分 ZAOB,D、E 在 OA、OB 上(2)CD+CE=OD+OE=<2OC(3)S=S+S=10C2四边形 ODCE△OCE△OCD22、全等型—120°S=S+S四边形 ODCE△OCE△OCD(五)、半角问题秘籍:角含半角要旋转251、对角互补之全等模型的相关结论在 ZAOB 中,C 是其中任意一点,过 C 向两边做垂线,垂足分别为 E、D,已知(1)ZAOB+ZACB=180。,(2)OC 平分 ZAOB...