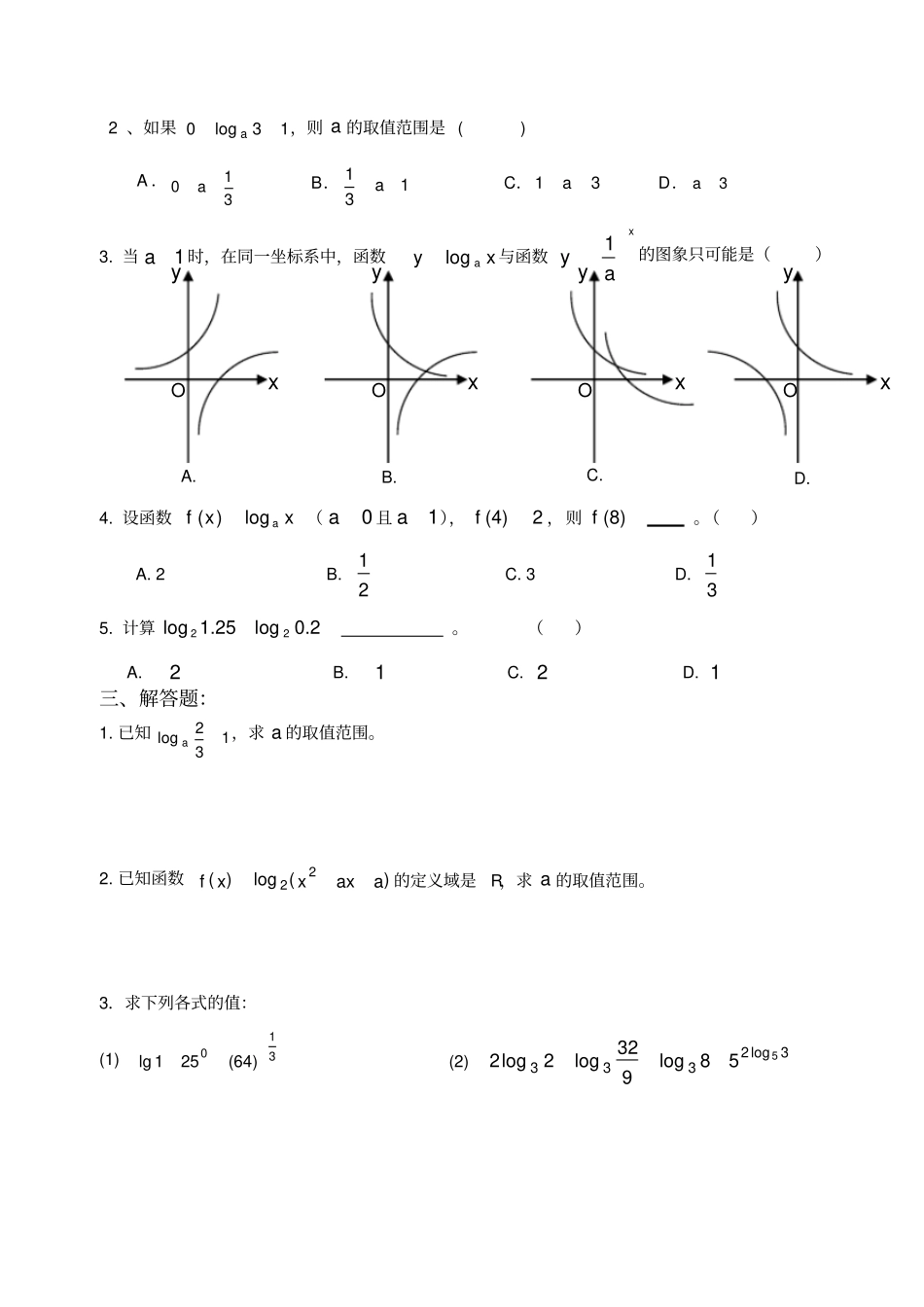
对数函数练习一、填空:1.对数的运算法则: (0,0 NM)⑴)(logMNa,⑵NMalog,⑶Malog,(4) 换底公式:bNaaloglog。2.计算:(1) yaalog;(2)1log a;(3) aalog;(4)xa alog; (5) 25lg4lg;(6) 3log 22;(7) 3ln2e= ;(8) 2log6log33= ;(9) 27log 3= ;(10)64log9log98= 。3.形如xyalog(0,1,0xaa)的函数叫做函数。其图象过定点,当时,是增函数;当时,是减函数。4.比较大小:⑴7.0log3___5.0log3(2)4.5log8.0____5.4log8.0⑶76log2___0 ⑷3log2___1 5.)4(logxya的定义域为;xy3log1的定义域为。6. 方程222 280xx的解 x =______________ 。二、选择题:1、函数xy2log和xy2 在同一坐标系中图象之间的关系是( )A .关于 x 轴对称B.关于 y 轴对称C.关于原点轴对称D.关于xy轴对称 2 、如果13log0a,则 a 的取值范围是 ( )A .310aB.131aC.31aD.3a3. 当1a时,在同一坐标系中,函数log ayx 与函数1xya的图象只可能是()4. 设函数( )log af xx (0a且1a),(4)2f,则(8)f。()A. 2 B. 12C. 3 D. 135. 计算22log 1.25log 0.2。()A. 2B. 1C. 2D. 1三、解答题:1. 已知132log a,求 a 的取值范围。2. 已知函数)(log)(22aaxxxf的定义域是R,求 a 的取值范围。3.求下列各式的值:(1)310)64(251lg(2)3log2333558log932log2log2xyOxyOxyOxyOA. B. C. D. 4.已知6log 20.3869 ,求6log 3