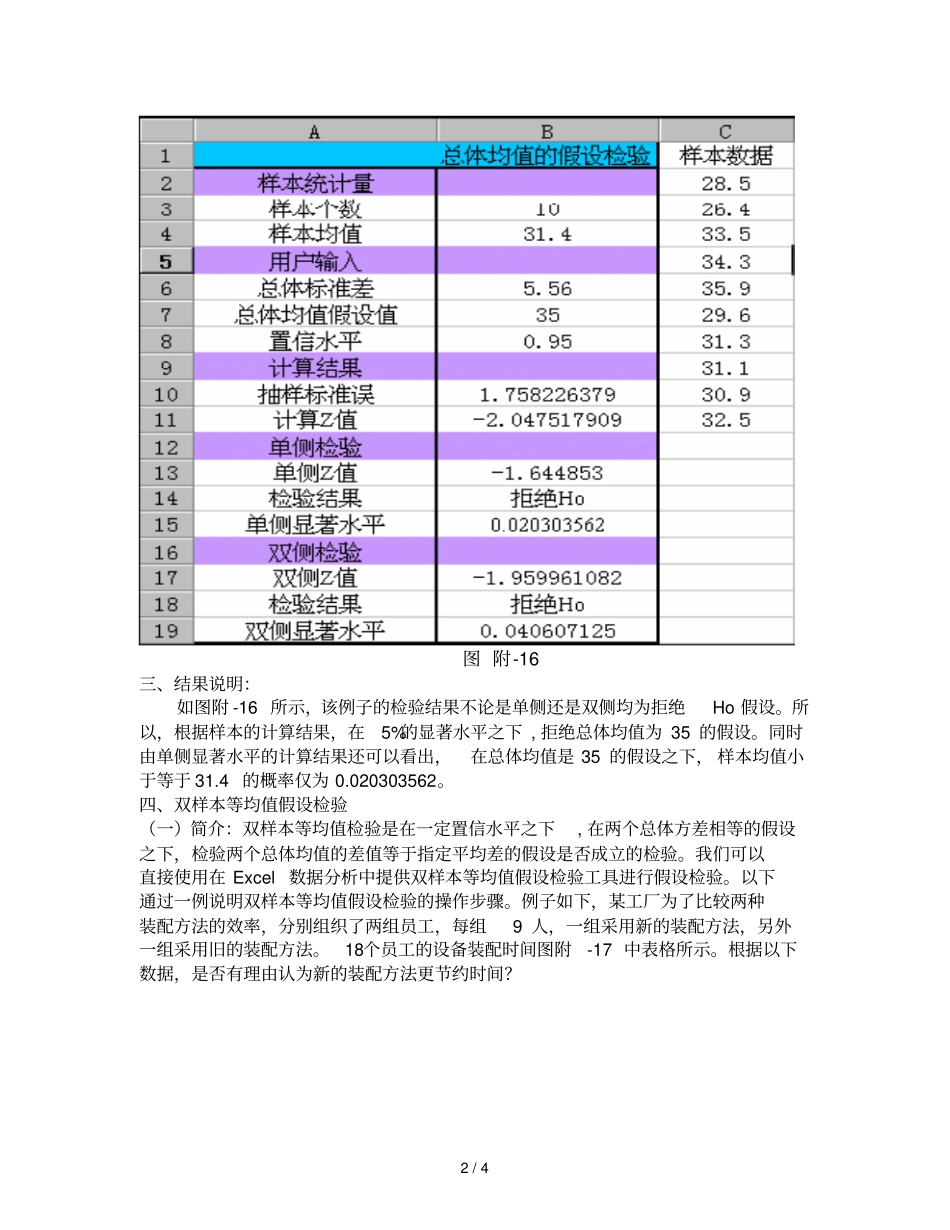
1 / 4 [ 实训四 ] 假设检验一、简介:假设检验是统计推断中的重要内容。以下例子利用Excel 的正态分布函数NORMSDIST、判断函数 IF 等,构造一张能够实现在总体方差已知情况下进行总体均值假设检验的 Excel 工作表。二、操作步骤:1.构造工作表。 如图附 -15 所示,首先在各个单元格输入以下的内容,其中左边是变量名,右边是相应的计算公式。2. 为表格右边的公式计算结果定义左边的变量名。选定A3:B4,A6:B8 ,A10:A11,A13:A15 和A17:B19 单元格,选择“插入”菜单的“名称”子菜单的“指定”选项,用鼠标点击“最左列”选项, 然后点击“确定”按扭即可。图 附-15 3.输入样本数据, 以及总体标准差、 总体均值假设、 置信水平数据。 如图附 -16 所示。4.为样本数据命名。选定 C1:C11 单元格,选择“插入”菜单的“名称”子菜单的“指定”选项,用鼠标点击“首行”选项, 然后点击“确定”按扭,得到如图附-16 中所示的计算结果。2 / 4 图 附-16三、结果说明:如图附 -16 所示,该例子的检验结果不论是单侧还是双侧均为拒绝Ho 假设。所以,根据样本的计算结果,在5%的显著水平之下 , 拒绝总体均值为 35 的假设。同时由单侧显著水平的计算结果还可以看出,在总体均值是 35 的假设之下, 样本均值小于等于 31.4 的概率仅为 0.020303562。四、双样本等均值假设检验(一)简介:双样本等均值检验是在一定置信水平之下, 在两个总体方差相等的假设之下,检验两个总体均值的差值等于指定平均差的假设是否成立的检验。我们可以直接使用在 Excel 数据分析中提供双样本等均值假设检验工具进行假设检验。以下通过一例说明双样本等均值假设检验的操作步骤。例子如下,某工厂为了比较两种装配方法的效率,分别组织了两组员工,每组9 人,一组采用新的装配方法,另外一组采用旧的装配方法。18个员工的设备装配时间图附-17 中表格所示。根据以下数据,是否有理由认为新的装配方法更节约时间?3 / 4 图 附 -17 (二)操作步骤:以上例子可按如下步骤进行假设检验。1. 选择“工具”菜单的“数据分析”子菜单,双击“t- 检验 : 双样本等方差假设”选项,则弹出图附 -18 所示对话框。图 附-18 4 / 4 图 附-19 2. 分别填写变量 1 的区域:$B$1:$B$10,变量 2 的区域: $D$1:$D$10,由于我们进行的是等均值的检验, 填写假设平均差为 0,由于数据的首行包括标志项选择标志选项,所以选...