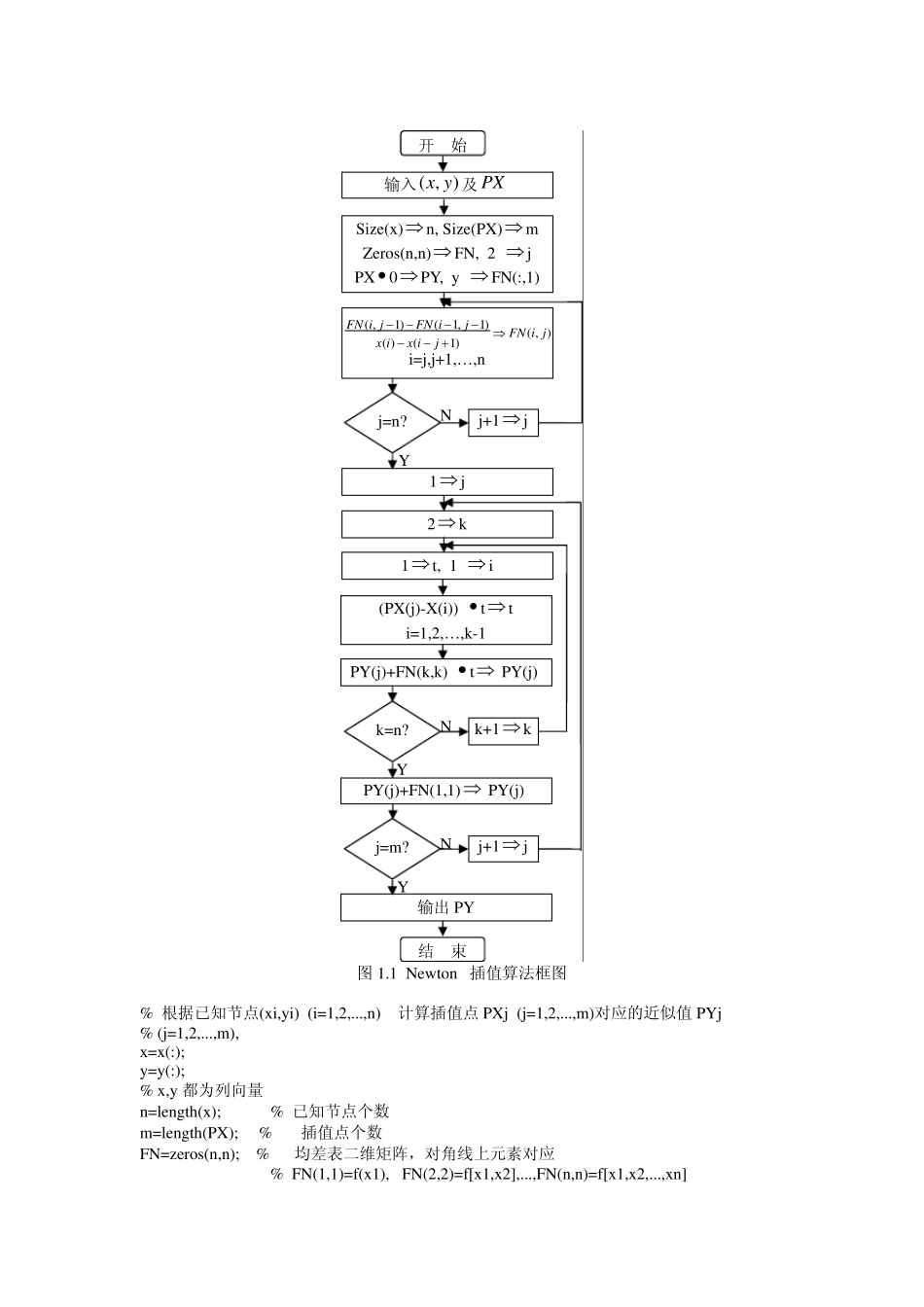
New ton 插值的算法实现 Lagrange 插值公式结构紧凑,便于理论分析。利用插值基函数也容易到插值多项式的值。Lagrange 插值公式的缺点是,当插值节点增加,或其位置变化时,全部插值基函数均要随之变化,从而整个插值公式的结构也发生变化,这在实际计算中是非常不利的。下面引入的New ton 插值公式可以克服这个缺点。 1、问题描述 当n=1 时,由点斜式直线方程知,过两点00(,())xf x和11( ,())x f x的直线方程为 1010010()()( )()().f xf xN xf xxxxx−=+−− 若记 100110( )()[,],f xf xf x xxx−=−则可把1( )N x 写成 10010( )()[,]().N xf xf x xxx=+− 显然,1( )N x 就是一次 Lagrange 插值多项式1( )L x 。由于1( )yN x=表示通过两点00(,())xf x和11( ,())x f x的直线,因此一次插值亦称为线性插值。 当n=2 时,进而记 120121120122121[ ,][,]()( )[ ,], [,,]f x xf x xf xf xf x xf x x xxxxx−−==−− 类似地,构造不超过二次的多项式 2001001201( )()[,]()[,,]()().Nxf xf x xxxf x x xxxxx=+−+−− 容易检验,这样的2( )Nx 满足插值条件 200211222()() ,( )( ) ,()() .Nxf xNxf xNxf x=== 因 此 ,2( )Nx 就 是二 次L a g r a n g e插值多项式2( )L x 。二次插值的几何解释是,用通过三点00(,())xf x,11( ,())x f x,22(,())xf x的抛物线2( )yNx=来近似所考察的曲线( )yf x=,因此这类插值亦称为抛物线插值。 从上述公式可见, 2101201( )( )[,,]()().NxN xf x x xxxxx=+−− 这种递推性,对于数值计算是很有效的。下面给出一般的计算公式。 2、New ton 插值多项式 为进一步构造更一般的插值多项式,记 10( )()kkiixxxω−==−∏ 由此构造 0011( )()[,,,]( )nnkkkNxf xf x xxxω==+∑L (1.1) 其中 12011010[ ,,,][,,,][,,,]kkkkf x xxf x xxf x xxxx−−=−LLL (1.2) 称之为( )f x 在01,,,kx xxL上的k 阶均差(或差商)。 显然,( )nNx 是次数不超过n 次的多项式,并由式(1.1)可知,它满足插值条件 ( )( ),0,1,, .niiNxf xin==L 因此把式(1.1)称作n 次Newton 插值多项式。根据插值多项式的惟一性,( )nNx 就是( )nL x 。 进一步地,有插值余项的均差型余项 011( )( )( )[ ,,,,]( ).nnnnR xf xNxf x x xxxω+=−=L (1.3) 在实...