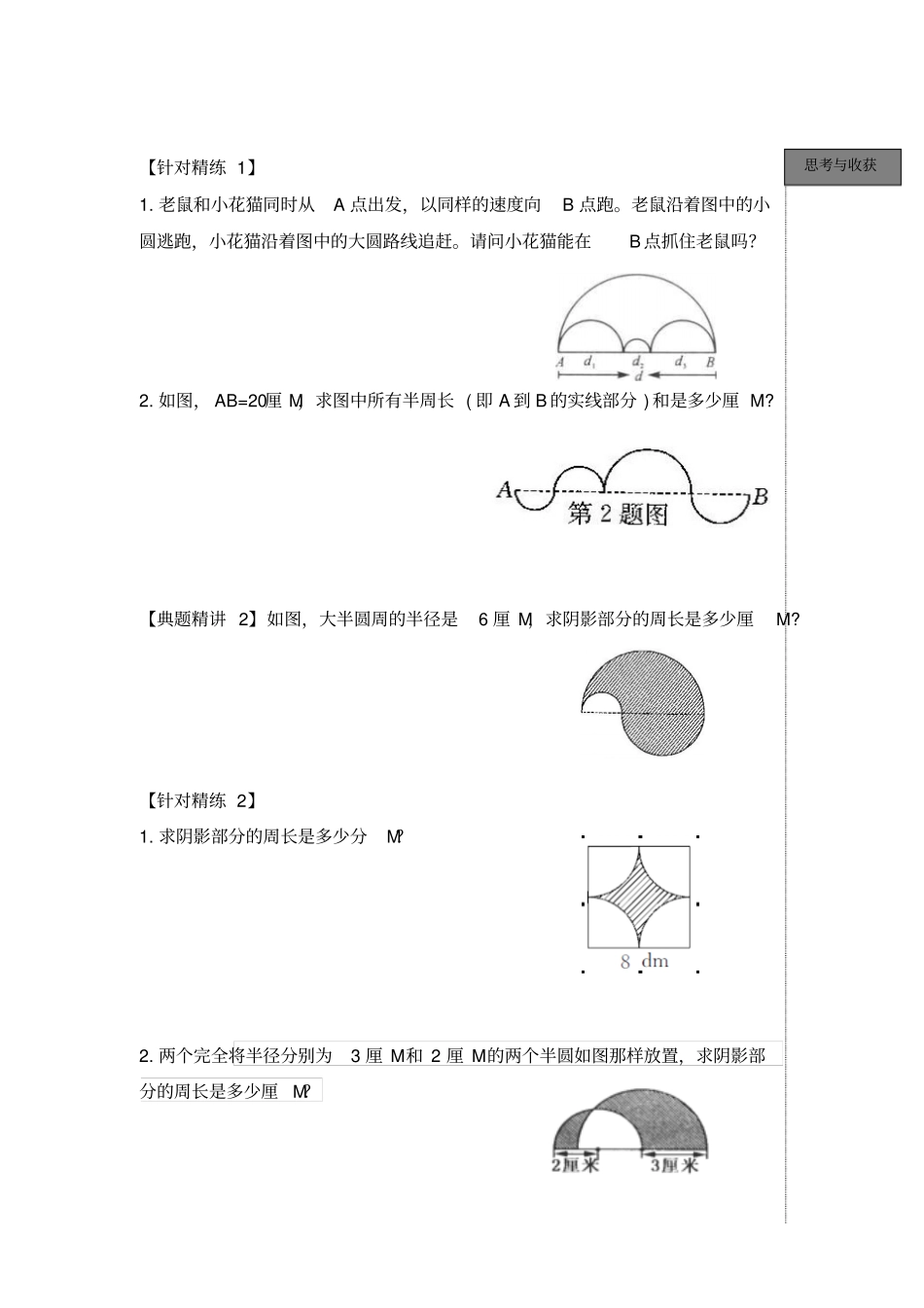
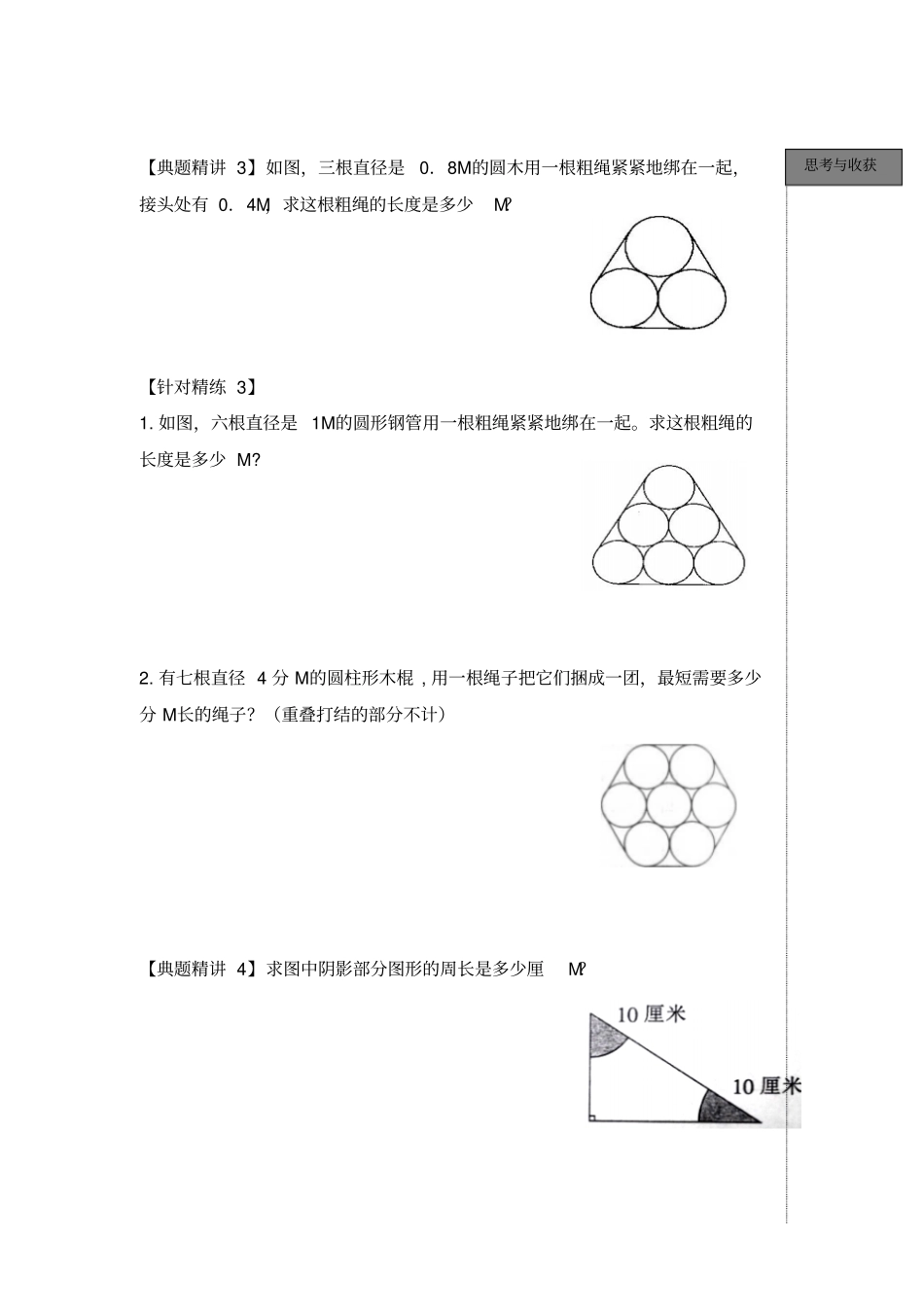
第一讲特殊图形周长(与圆相关)1.圆是平面上的曲线图形,也是我们第一次学习曲线图形。在这一讲中,我们将要学习这种特殊图形的周长和面积的应用。我们已经知道圆的周长和面积的基本计算方法: S圆 =∏r2 ,C圆 =2∏r= ∏d;对于教材选学的扇形,我们也可以得出其面积和周长的计算方法:2.圆是轴对称图形,所以我们在计算圆的面积时还可以运用割补、平移、旋转等方法将不规则的图形转化成规则图形来解决。3.圆周率是一个无限不循环小数,本书中如无特殊说明,圆周率都取∏=3.14。【典题精讲 1】如图,两只蚂蚁都要从A 点爬到 B 点,有两条路可以走,甲蚂蚁爬的是一个大半圆周 ( 图中细线 ) ,乙蚂蚁爬的是三个小半圆周( 图中粗黑线部分) ,聪明的你能比一比哪一只蚂蚁爬的路线更近一些吗? 【结论】 几个小圆直径相加等于最大圆的直径时,就可以说小圆的周长和等于大圆的周长。另外,半圆的周长和圆周长的一半是不相同的。专题解读精讲与精练思考与收获【针对精练 1】1. 老鼠和小花猫同时从A 点出发,以同样的速度向B 点跑。老鼠沿着图中的小圆逃跑,小花猫沿着图中的大圆路线追赶。请问小花猫能在B 点抓住老鼠吗?2. 如图, AB=20厘 M,求图中所有半周长 ( 即 A 到 B 的实线部分 ) 和是多少厘 M? 【典题精讲 2】如图,大半圆周的半径是6 厘 M,求阴影部分的周长是多少厘M? 【针对精练 2】1. 求阴影部分的周长是多少分M?2. 两个完全将半径分别为3 厘 M和 2 厘 M的两个半圆如图那样放置,求阴影部分的周长是多少厘M?思考与收获【典题精讲 3】如图,三根直径是0.8M的圆木用一根粗绳紧紧地绑在一起,接头处有 0.4M,求这根粗绳的长度是多少M?【针对精练 3】1. 如图,六根直径是 1M的圆形钢管用一根粗绳紧紧地绑在一起。求这根粗绳的长度是多少 M? 2. 有七根直径 4 分 M的圆柱形木棍 , 用一根绳子把它们捆成一团,最短需要多少分 M长的绳子?(重叠打结的部分不计)【典题精讲 4】求图中阴影部分图形的周长是多少厘M?思考与收获【针对精练 4】1. 图中每个扇形的半径是3 厘 M,求阴影部分图形的周长是多少厘M?(单位:厘 M)2. 1. 一个大圆内有三个大小不同的小圆(如图),这些小圆的圆心在大圆的同一条直径上,连同大圆在内每相邻的两个圆都相切,已知大圆的半径是10 厘M,求三个小圆的周长和是多少厘M?2. 求图中所示阴影部分的周长是多少厘M?家庭作业思考与收...