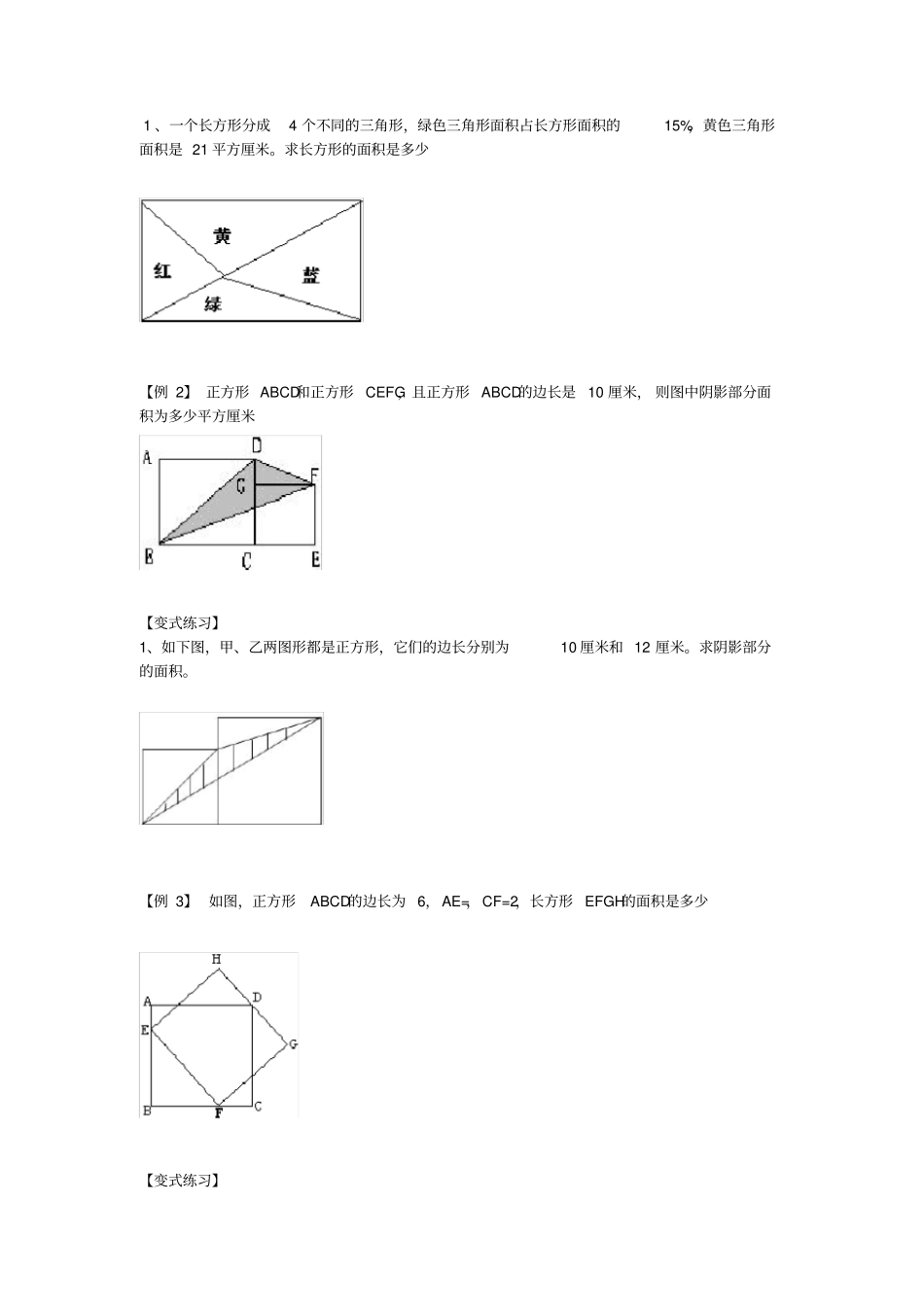
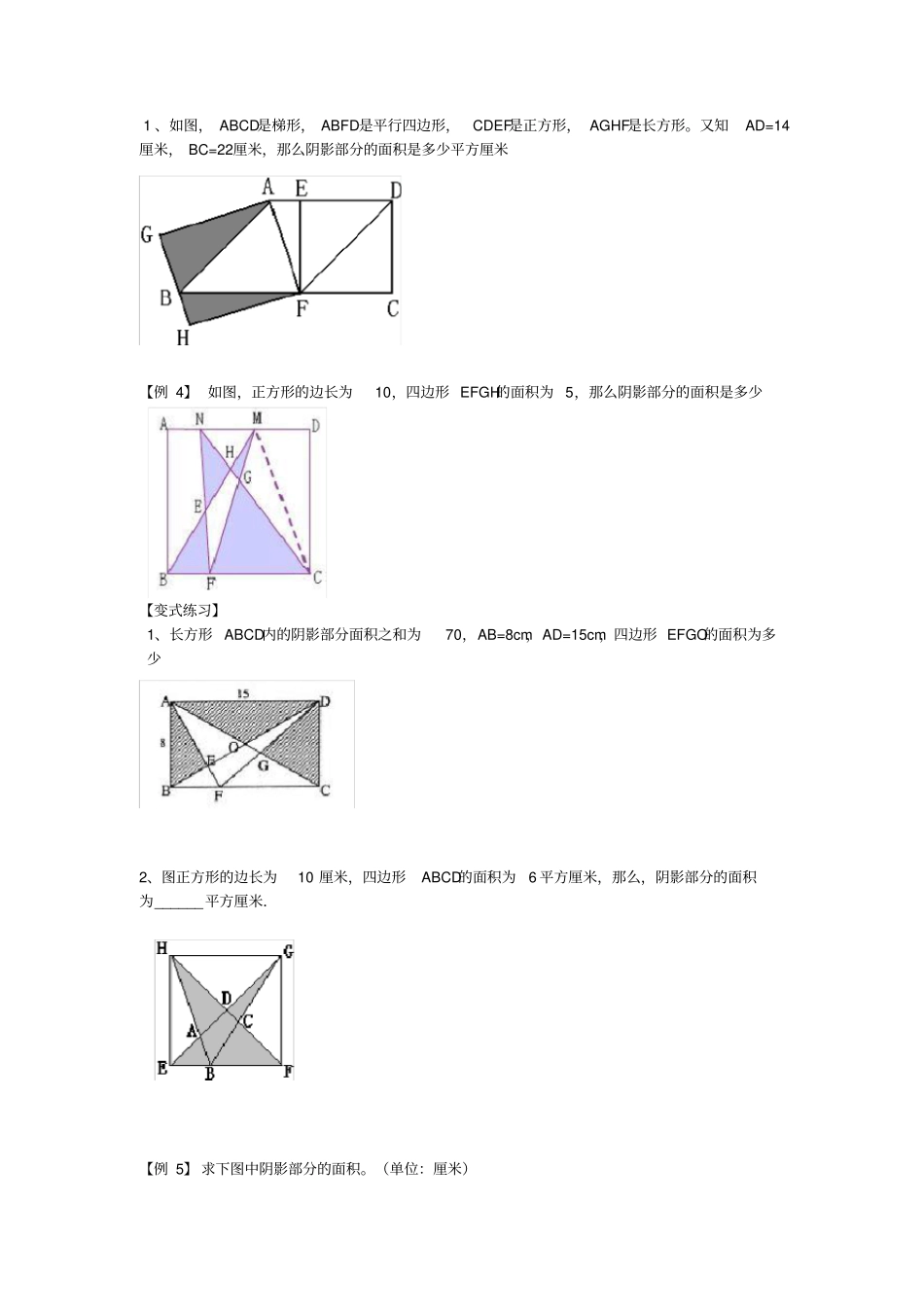
OFEDCBA第 43 讲燕尾模型和等积变换1、考察范围: ①多边形面积计算公式;②图形的折叠与对称;③几何模型与面积计算结合。2、考察重点: 能灵活运用和差法、转换法、 割补法和等积变换及相应几何模型解面积问题。3、命题趋势: 主要以转换法、割补法和等积变换模型来进行考察的题型比较多,并要求结合多边形的面积公式来计算结果。1、公式边长边长正方形S宽长长方形S高底平行四边形S2高下底)(上底梯形S高底底高高底三角形三角形三角形222SSS2、方法①和差法: 通过观察, 分析出不规则图形的面积是由哪些规则图形组合而成的,再利用这些规则图形的面积的和与差来求面积。②割补法 :将不规则图形割补拼接成规则图形,利用规则图形的面积公式计算。③转换法 :通过平移、旋转、对称等方法将不规则图形转化成面积相等的规则图形。④等积变换模型:相等面积或等体积之间的图形变形。⑤燕尾定理:如图,在三角形ABC中, AD , BE , CF 相交于同一点O ,那么有如下结论::ABOACOSSBDDC上述定理给出了一个新的转化面积比与线段比的手段,因为ABO 和ACO 的形状很象燕子的尾巴,所以这个定理被称为燕尾定理 .该定理在许多几何题目中都有着广泛的运用,它的特殊性在于, 它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.【例 1】如图, ABFE和 CDEF都是矩形, AB的长是 4 厘米, BC的长是 3 厘米,那么图中阴影部分的面积是多少【变式练习】考点解读知识梳理典例剖析 1 、一个长方形分成4 个不同的三角形,绿色三角形面积占长方形面积的15%,黄色三角形面积是 21 平方厘米。求长方形的面积是多少【例 2】 正方形 ABCD和正方形 CEFG,且正方形 ABCD的边长是 10 厘米, 则图中阴影部分面积为多少平方厘米【变式练习】1、如下图,甲、乙两图形都是正方形,它们的边长分别为10 厘米和 12 厘米。求阴影部分的面积。【例 3】 如图,正方形ABCD的边长为 6,AE=,CF=2,长方形 EFGH的面积是多少【变式练习】 1 、如图, ABCD是梯形, ABFD是平行四边形,CDEF是正方形, AGHF是长方形。又知AD=14厘米, BC=22厘米,那么阴影部分的面积是多少平方厘米【例 4】 如图,正方形的边长为10,四边形 EFGH的面积为 5,那么阴影部分的面积是多少【变式练习】1、长方形 ABCD内的阴影部分面积之和为70,AB=8cm,AD=15cm,四边形 EFGO的面积为多少2、图正方形的边长为...