冲激信号δ(t)的三种定义与相关性质的简单讨论VIP免费

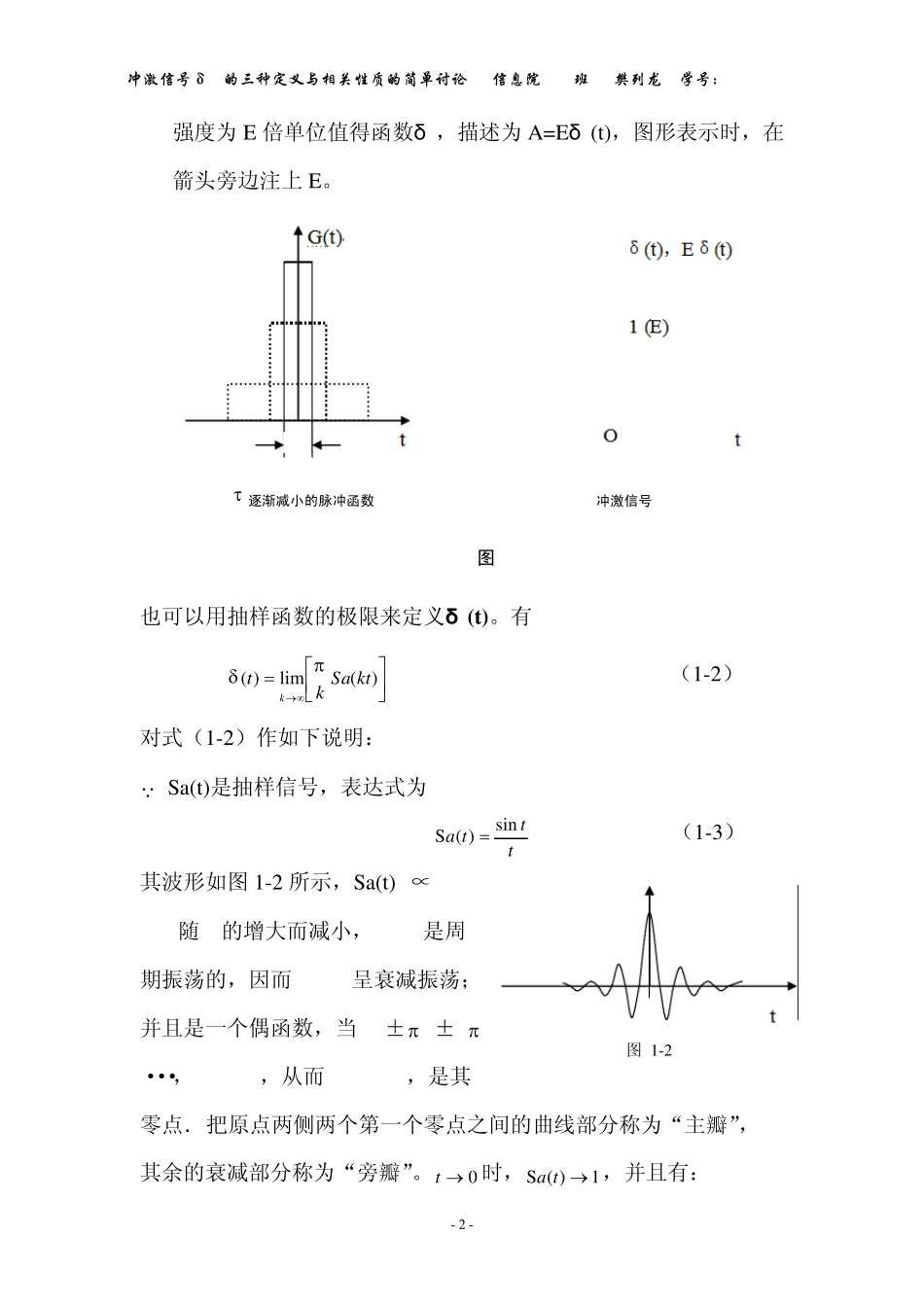
冲激信号δ(t)的三种定义与相关性质的简单讨论 信息院 1132班 樊列龙 学号：0909113224 - 1 - 冲激信号δ(t)的三种定义与相关性质的简单讨论 信息科学与工程学院 1132 班 樊列龙 学号：0909113224 有一些物理现象，如理学中的爆炸、冲击、碰撞······，电学中的放电、闪电雷击等，它们都有共同特点： ① 持续时间短. ② 取值极大. 冲击函数（或冲击信号）就是对这些物理现象的科学抽象与描述。通常用δ (t)表示冲激信号，它是一个具有有限面积的窄而高的尖峰信号，它也可以被称作δ 函数或狄拉克（Dirac）函数，在信号领域中占有非常重要的地位. 由于冲激函数的特殊性，现给出其两种不严格的定义如下： 定义一：用脉冲函数极限定义冲激信号. 如图 1-1(a)的矩形脉冲，宽为τ ，高为τ1 ，其面积为 A.当 A=1 称之为单位冲激信号. 现保持脉冲面积不变，逐渐减小τ ，则脉冲的幅度逐渐增大，当0时，矩形脉冲的极限成为单位冲激函数，即：   221lim)(0ttt （1-1） 冲击信号的波形就如1-1(b)所示. δ (t)只表示在 t=0 点有“冲激”，在 t=0 点以外的各处函数值均为 0，其冲激强度（冲激面积）为 1，若为 A 则表示一个冲击冲激信号δ(t)的三种定义与相关性质的简单讨论 信息院 1132班 樊列龙 学号：0909113224 - 2 - 图 1-2 强度为E 倍单位值得函数δ ，描述为A=Eδ (t)，图形表示时，在箭头旁边注上E。 也可以用抽样函数的极限来定义δ (t)。有 )(lim)(ktSaktk （1-2） 对式（1-2）作如下说明：  Sa(t)是抽样信号，表达式为 tttasin)(S （1-3） 其波形如图1-2 所示，Sa(t) ∝1/t, 1/t随t的增大而减小，sint是周 期振荡的，因而Sa(t)呈衰减振荡； 并且是一个偶函数，当t=± ,±2 , ···，sint=0，从而Sa(t)=0，是其 零点． 把原点两侧两个第一个零点之间的曲线部分称为“主瓣”， 其余的衰减部分称为“旁瓣”。0t时， 1)(Sta，并且有： (a) 逐渐减小的脉冲函数 (b)冲激信号 图 1-1 冲激信号δ(t)的三种定义与相关性质的简单讨论 信息院 1132班 樊列龙 学号：0909113224 - 3 - 图 1-3 02)(dttSa 因其是偶函数有  dttSa )( （1-4） 由式（1-4）知 1)()()(dtktSakktd...