几何光学习题及解答VIP免费

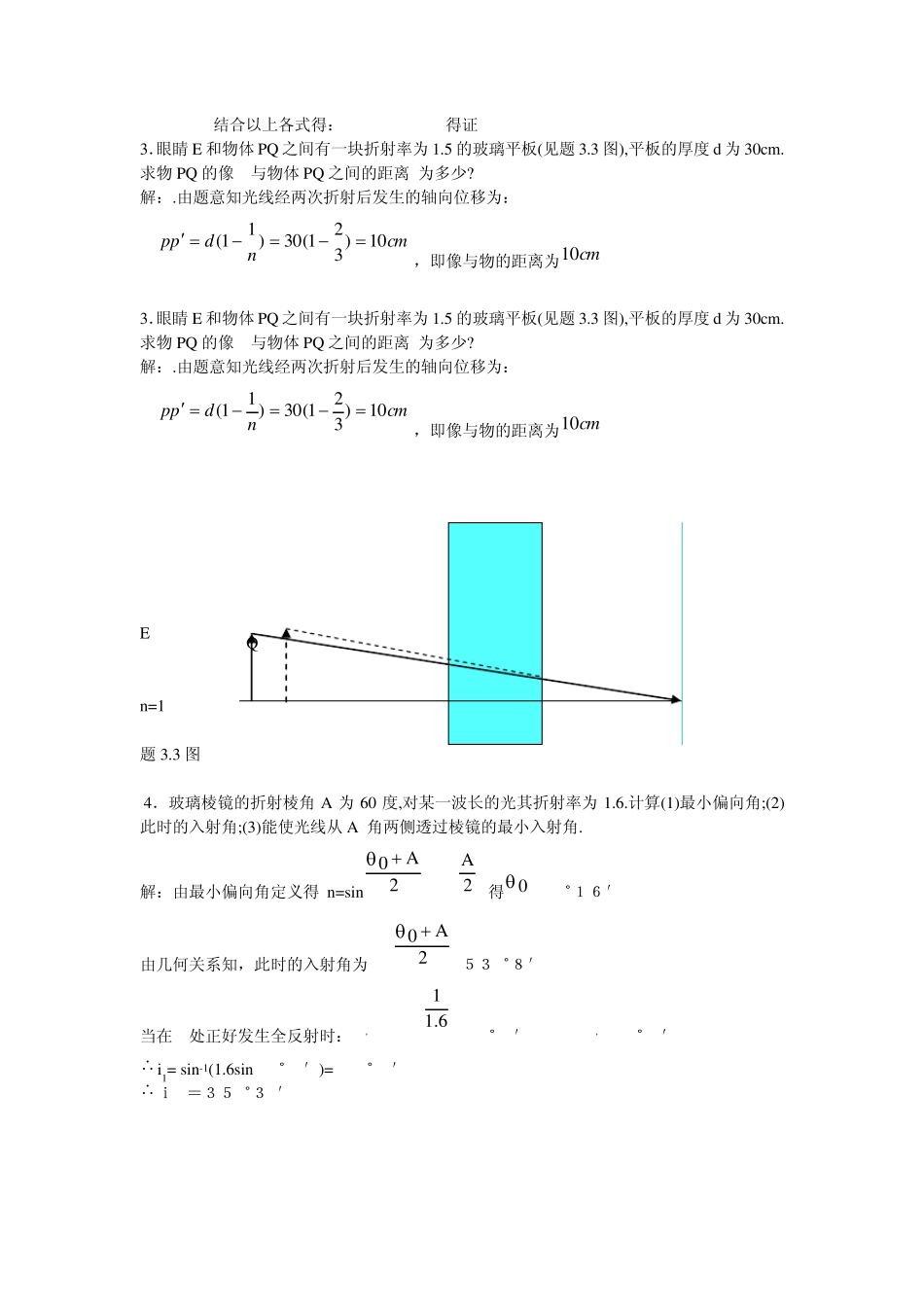
几何光学习题及解答 1．证明反射定律符合费马原理。 证明：费马原理是光沿着光程为最小值、最大值或恒定值的路径传播。 BAnds或恒值max.min，在介质n与'n 的界面上，入射光A 遵守反射定律11ii, 经O点到达B点，如果能证明从A点到B点的所有光程中AOB是最小光程，则说明反射定律符合费马原理。 设C点为介质分界面上除O点以外的其他任意一点，连接ACB并说明光程 ACB>光程 AOB 由于 ACB 与 AOB 在同一种介质里，所以比较两个光程的大小，实际上就是比较两个路程ACB与AOB的大小。 从B点到分界面的垂线，垂足为o ，并延长OB  至 B′，使BOBO，连接 BO  ，根据几何关系知 BOOB，再结合11ii，又可证明∠180BAO°，说明BAO  三点在一直线上，BAO  与AC和 BC  组成ΔBAC  ，其中BCACBAO。 又 CBBCAOBOBAOBOAOBAO, ACBCBACAOB 即符合反射定律的光程AOB是从A点到B点的所有光程中的极小值，说明反射定律符合费马原理。 2、根据费马原理可以导出在近轴光线条件下，从物点发出并会聚到像点的所有光线的光程都相等.由此导出薄透镜的物象公式。 证明：由QBA～FBA得：OF\AQ=BO\BQ=f\s 同理，得 OA\BA=f  \s,BO\BA=f\s 由费马定理：NQA+NQA =NQQ C A O B O‘ B‘ i’ n n’ 结合以上各式得：(OA+OB)\BA=1得证 3．眼睛E 和物体PQ 之间有一块折射率为1.5 的玻璃平板(见题3.3 图),平板的厚度d 为30cm.求物PQ 的像 与物体PQ 之间的距离 为多少? 解：.由题意知光线经两次折射后发生的轴向位移为： cmndpp10)321(30)11(，即像与物的距离为cm10 3．眼睛E 和物体PQ 之间有一块折射率为1.5 的玻璃平板(见题3.3 图),平板的厚度d 为30cm.求物PQ 的像 与物体PQ 之间的距离 为多少? 解：.由题意知光线经两次折射后发生的轴向位移为： cmndpp10)321(30)11(，即像与物的距离为cm10 E n=1 题3.3 图 4．玻璃棱镜的折射棱角A 为60 度,对某一波长的光其折射率为1.6.计算(1)最小偏向角;(2)此时的入射角;(3)能使光线从A 角两侧透过棱镜的最小入射角. 解：由最小偏向角定义得 n=sin2A0 /sin2A,得 0 =46゜１６′ 由几何关系知，此时的入射角为:i=2A0 =５３゜８′ 当在C处正好发生全反射时：i2’= sin-1 6.11 =38゜41′,i2=A- i2’=21゜19′  i1= si...