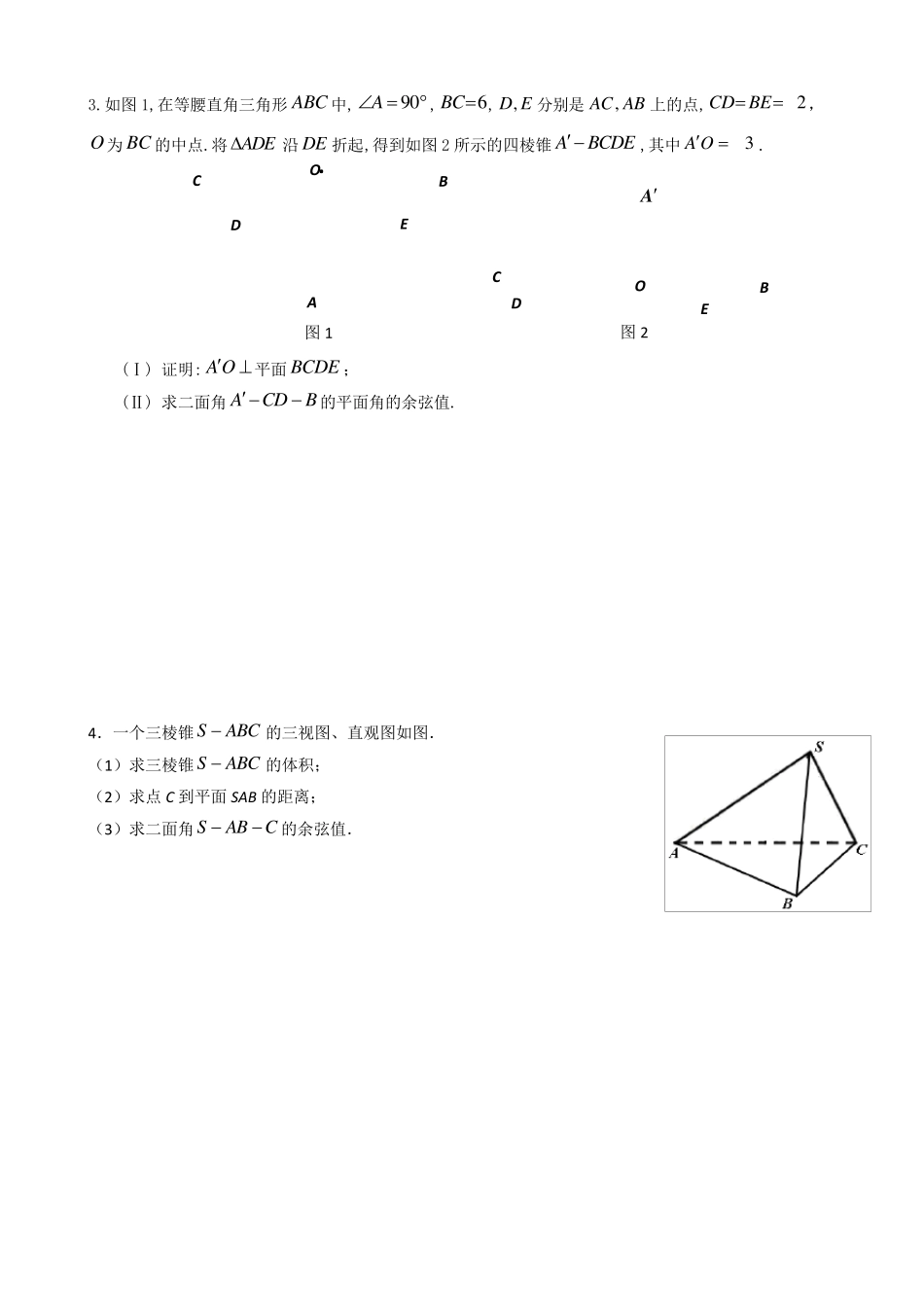
6.3 二面角 一、作点在面上的射影(作垂线) 1、已知矩形ABCD 中,10AB ,6BC ,将矩形沿对角线BD把ABD折起,使A移到1A 点,且1A在平面BCD 上的射影O 恰好在CD 上. (Ⅰ)求证:1BCA D; (Ⅱ)求证:平面1A BC 平面1A BD ; (Ⅲ)求二面角CBDA1的余弦值. 2、在如图所示的几何体中,四边形ABCD 是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF。 (Ⅰ)求证:BD⊥平面AED; (Ⅱ)求二面角F-BD-C 的余弦值。 3.如图1,在等腰直角三角形ABC 中,9 0A ,6BC ,,D E 分别是,AC AB 上的点,2CD BE, O为BC 的中点.将ADE沿DE 折起,得到如图2 所示的四棱锥ABCDE,其中3A O. (Ⅰ) 证明: A O 平面 BCDE ; (Ⅱ) 求二面角ACDB的平面角的余弦值. 4.一个三棱锥SABC的三视图、直观图如图. (1)求三棱锥SABC的体积; (2)求点C 到平面 SAB 的距离; (3)求二面角SABC的余弦值. . C O B D E A C D O B E A 图1 图2 二、过棱作垂面(线)法(作垂面) 1.在锥体PABCD中,ABCD 是边长为1 的棱形,且06 0DAB,2PAPD,2 ,PB ,E F分别是,BC PC 的中点, (1)证明:ADDEF 平面; (2)求二面角PADB的余弦值. 2、如图,边长为2 的正方形ABCD,E,F 分别是AB,BC 的中点,将△AED,△DCF 分别沿DE,DF 折起,使A,C两点重合于A。 (1)求证:A D ⊥EF; (2)求二面角AEFD的余弦值. _ F_ F_ D _ E_ B _ A _ E_ A _ / _ D _ C _ B 3 、如图,四棱锥P-ABCD 的底面ABCD 是正方形,PD⊥平面ABCD,E 为PB 上的点,且2BE=EP。 (1)证明:AC⊥DE; (2)若PC=2 BC,求二面角E-AC-P 的余弦值。 4、 如图,在四棱锥P—ABCD中,底面是边长为2 3 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA= 2 6 , M,N 分别为PB,PD 的中点. (Ⅰ)证明:MN∥平面ABCD; (Ⅱ) 过点A 作 AQ⊥PC,垂足为点Q,求二面角A—MN—Q 的平面角的余弦值. 图4ABCA1C1B1DE三、无棱的延展半平面(作延长线或平行线) 1.如图4,在三棱柱111ABCA B C中,△ABC 是边长为2 的等边三角形, 1AA 平面ABC ,D ,E 分别是1CC ,AB 的中点. (1)求证:CE ∥平面1A BD ; (2)若 H 为1A B 上的动点,当CH 与平面1A AB 所成最大角的正切值为152时...