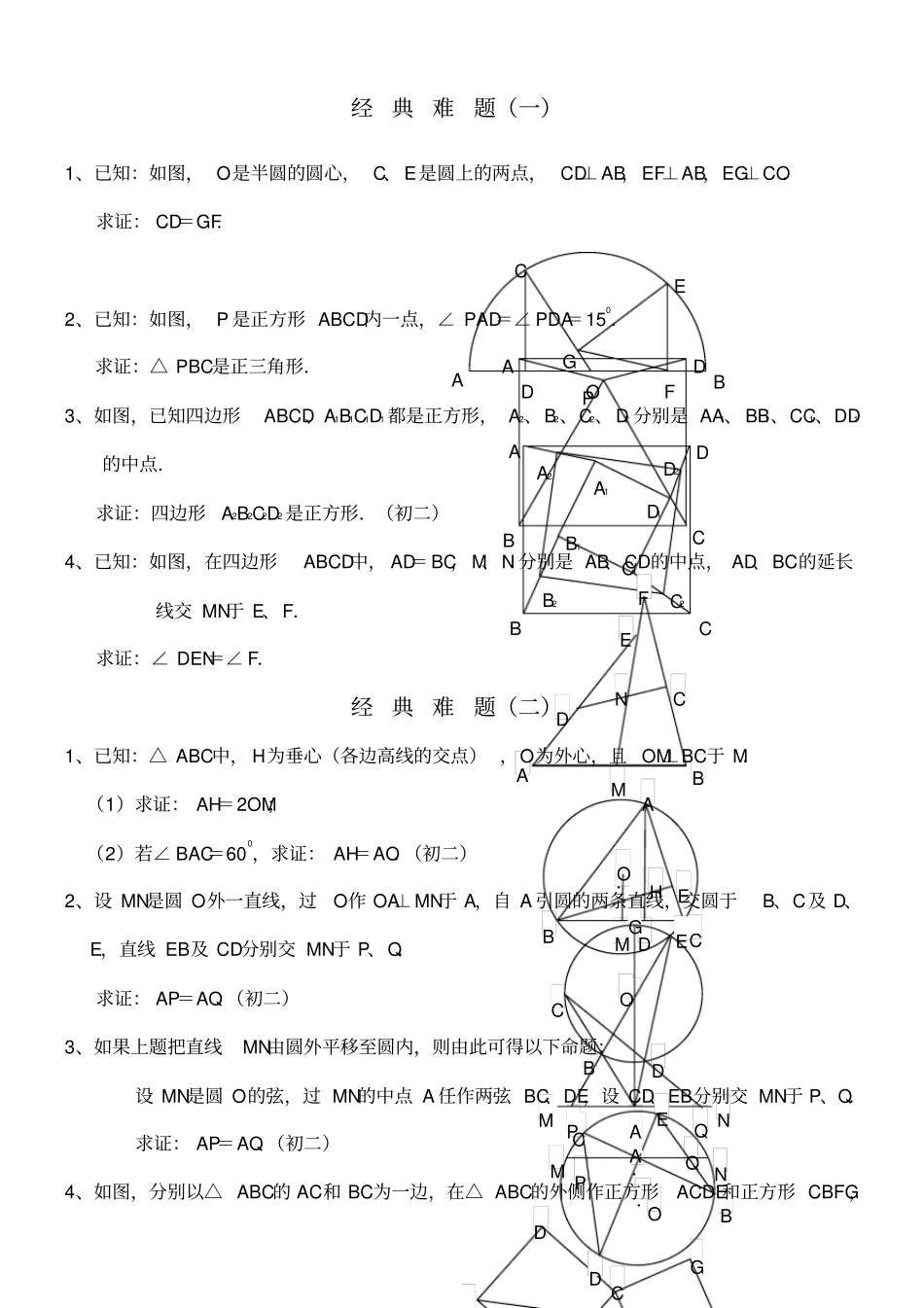
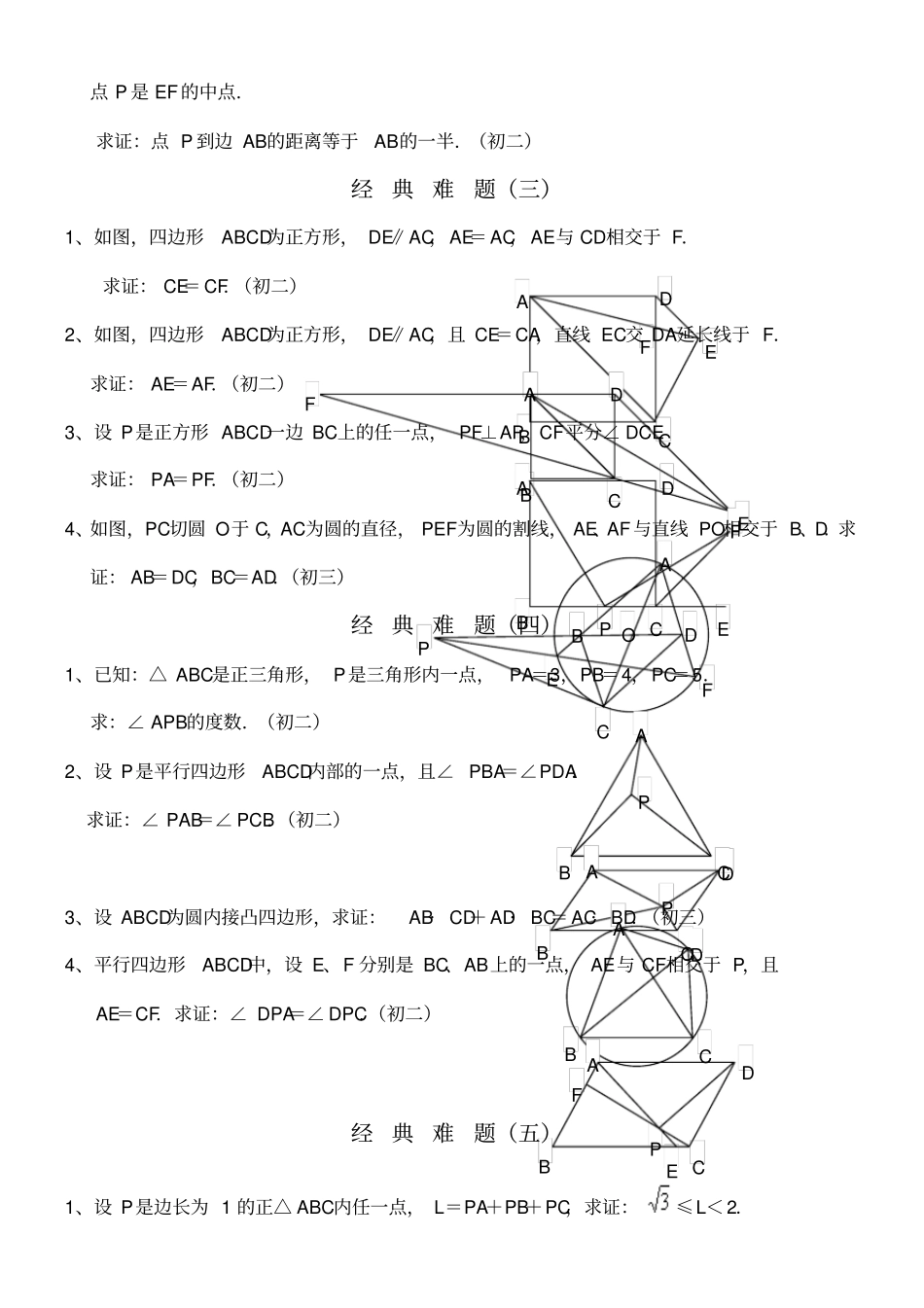
C G D 经典难题(一)1、已知:如图, O是半圆的圆心, C、 E是圆上的两点, CD⊥ AB,EF⊥AB,EG⊥CO.求证: CD=GF.2、已知:如图, P 是正方形 ABCD内一点,∠ PAD=∠ PDA=150.求证:△ PBC是正三角形.3、如图,已知四边形ABCD、A1B1C1D1 都是正方形, A2、B2、C2、 D2 分别是 AA1、 BB1、CC1、DD1的中点.求证:四边形A2B2C2D2 是正方形.(初二)4、已知:如图,在四边形ABCD中, AD= BC, M、N 分别是 AB、CD的中点, AD、BC的延长线交 MN于 E、F.求证:∠ DEN=∠ F.经典难题(二)1、已知:△ ABC中, H为垂心(各边高线的交点) ,O为外心,且 OM⊥BC于 M.(1)求证: AH=2OM;(2)若∠ BAC=600,求证: AH=AO.(初二)2、设 MN是圆 O外一直线,过O作 OA⊥ MN于 A,自 A 引圆的两条直线,交圆于B、C及 D、E,直线 EB及 CD分别交 MN于 P、Q.求证: AP=AQ.(初二)3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设 MN是圆 O的弦,过 MN的中点 A 任作两弦 BC、DE,设 CD、EB分别交 MN于 P、Q.求证: AP=AQ.(初二)4、如图,分别以△ ABC的 AC和 BC为一边,在△ ABC的外侧作正方形ACDE和正方形 CBFG,A P C D B A F G C E B O D D2 C2 B2 A2 D1 C1 B1 C B D A A1 A N F E C D M B ·A D H E M C B O ·G A O D B E C Q P N M · O Q P B D E C N M ·A 点 P 是 EF的中点.求证:点 P 到边 AB的距离等于AB的一半.(初二)经典难题(三)1、如图,四边形ABCD为正方形, DE∥AC,AE= AC, AE与 CD相交于 F.求证: CE= CF.(初二)2、如图,四边形ABCD为正方形, DE∥AC,且 CE=CA,直线 EC交 DA延长线于 F.求证: AE=AF.(初二)3、设 P是正方形 ABCD一边 BC上的任一点, PF⊥AP,CF平分∠ DCE.求证: PA=PF.(初二)4、如图,PC切圆 O于 C,AC为圆的直径, PEF为圆的割线, AE、AF与直线 PO相交于 B、D.求证: AB=DC,BC=AD.(初三)经典难题(四)1、已知:△ ABC是正三角形, P是三角形内一点, PA=3,PB=4,PC=5.求:∠ APB的度数.(初二)2、设 P是平行四边形ABCD内部的一点,且∠ PBA=∠PDA.求证:∠ PAB=∠ PCB.(初二)3、设 ABCD为圆内接凸四边形,求证:AB· CD+ AD·BC= AC· BD...