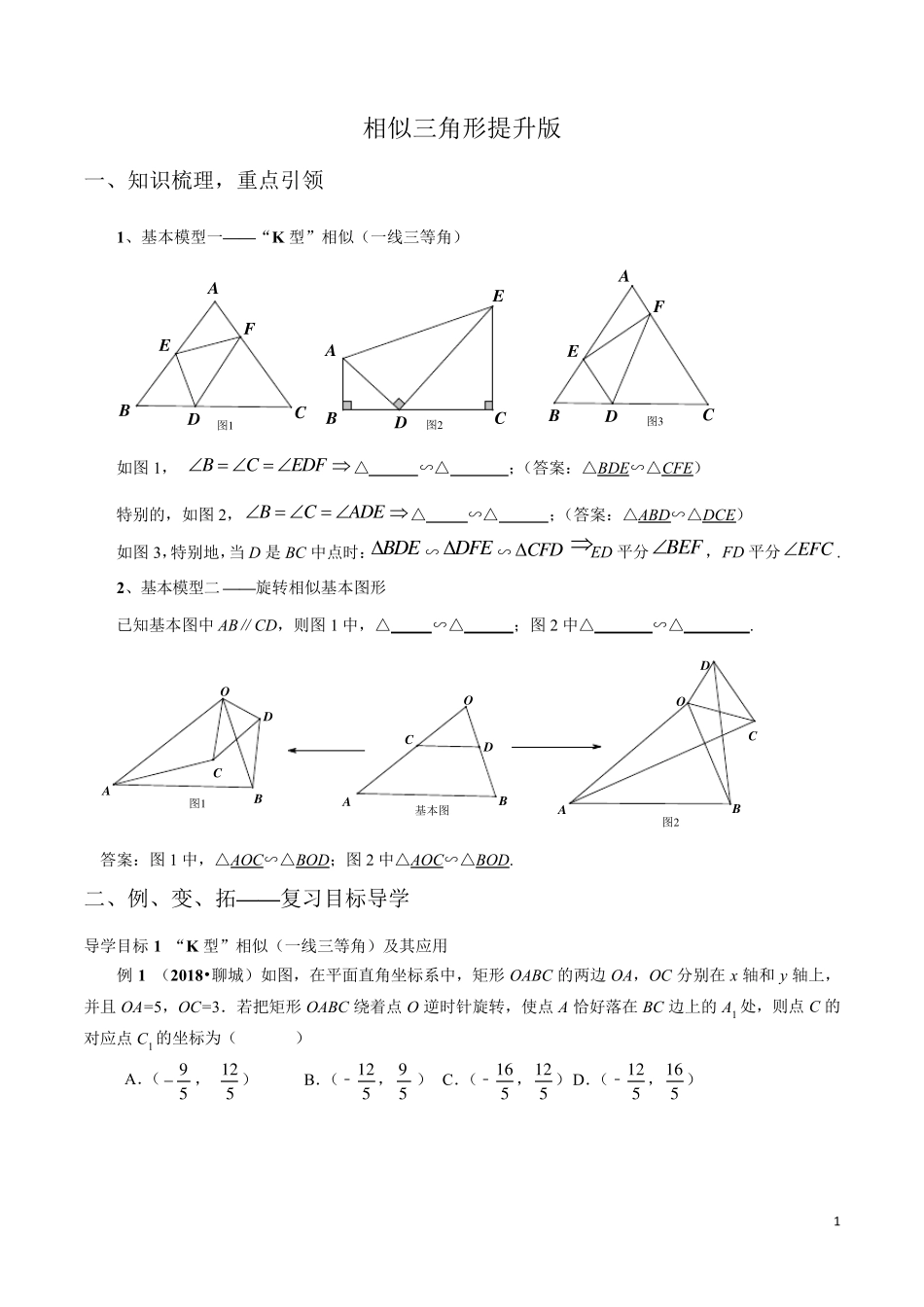
1 相似三角形提升版 一、知识梳理,重点引领 1、基本模型一— — “K 型”相似(一线三等角) 如图1, BCEDF △ ∽△ ;(答案:△BDE∽△CFE) 特别的,如图2,BCADE △ ∽△ ;(答案:△ABD∽△DCE) 如图3,特别地,当D 是BC 中点时:BDE∽DFE∽CFDED 平分BEF, FD 平分EFC. 2、基本模型二— — 旋转相似基本图形 已知基本图中AB∥CD,则图1 中,△ ∽△ ;图2 中△ ∽△ . 答案:图1 中,△AOC∽△BOD;图2 中△AOC∽△BOD. 二、例、变、拓— — 复习目标导学 导学目标1 “K 型”相似(一线三等角)及其应用 例1 (2018•聊 城 )如图,在 平面 直 角坐 标系 中,矩 形OABC 的两 边 OA,OC 分别在 x 轴 和y 轴 上 ,并 且 OA=5,OC=3. 若 把 矩 形OABC 绕 着 点O 逆 时针 旋转,使 点A 恰 好 落 在 BC 边 上 的A1 处 ,则点C 的对 应点C1 的坐 标为 ( ) A.(95, 1 25) B.(﹣ 1 25,95) C.(﹣ 1 65,1 25) D.(﹣ 1 25,1 65) 图3图2图1EEEBCBCCBADFADADF基本图图2图1DDDABOOBAABOCCC 2 【答案】A. 【思路分析】过点C1 作C1N⊥x轴于点N,然后利用相似三角形的判定与性质得出△ONC1 三边关系,再利用勾股定理列方程求解即可. 【试题解析】解:如图,过点C1 作C1N⊥x轴于点N,过点A1 作A1M⊥x轴于点M, 由题意可得:∠C1NO=∠A1MO=90°,∠1=∠2=∠3, 则△A1OM∽△OC1N, OA=5,OC=3,∴OA1=5,A1M=3,∴OM=4, ∴设 NO=3x,则 NC1=4x,OC1=3, 则(3x)2+(4x)2=9,解得:x=35(负数舍去),则 NO= 95,NC1=125, 故点C 的对应点C1 的坐标为(95,125).故选 A. 变式 1 如图,等边ABC中,D 是边BC 上的一点,且:1:3BD DC ,把 ABC折叠,使点A 落在BC 边上的点D 处.那么 AMAN的值为 . 【答案】57. 【解析】由翻折可得:,,AMDMANDNMDNA , 设1,3BDDC,则4,4BMDMCNDN, BDM∽ CND,∴4 154 37BDMCNDCAMDMANDNC. xyC1B1A1CBAOxy321MNC1B1A1CBAODABCMN 3 拓展1 如图,已知ABC中,9 0C ,2ACBC,O 是AB 的中点,将4 5 角的顶点置于点O, 并绕点O 旋转,使角的两边分别交边AC、BC 于点D、E,连接DE. (1)求证AOD∽OED;(2)...