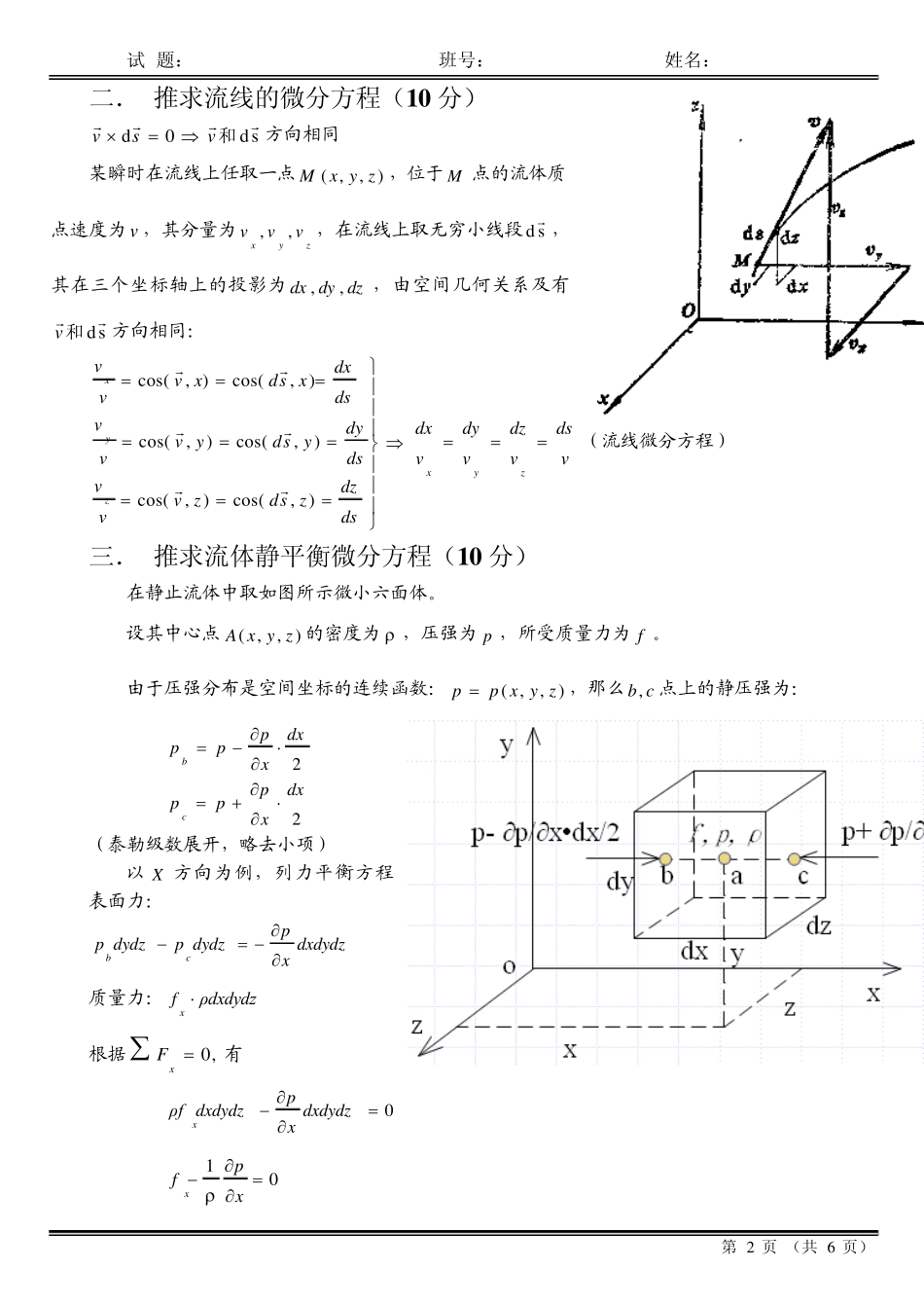
哈工大 2007 年秋季学期 工程流体力学(A 卷) 题号 一 二 三 四 五 六 七 总分 分数 第 1 页 (共 6 页) 班号 姓名 一.说明下列基本概念(30 分) 1. 连续介质模型 在流体力学的研究中,将实际由分子组成的结构用流体微元代替。流体微元有足够数量的分子,连续充满它所占据的空间,这就是连续介质模型。 2. 流体动力粘度和运动粘度 动力粘度:单位速度梯度时内摩擦力的大小 dzdv / 运动粘度:动力粘度和流体密度的比值 3. 断面平均流速和时间平均流速 流经有效截面的体积流量除以有效截面积而得到的商 Aqvva 在某一时间间隔内,以某平均速度流经微小过流断面的流体体积与以真实速度流经此微小过流断面的流体体积相等,该平均速度称为时间平均流速。 4. 层流、紊流 层流:定向的恒定流动 紊流:不定向混杂的流动 5. 沿程阻力、局部阻力 流体沿流动路程所受的阻碍称为沿程阻力 局部阻力之流体流经各种局部障碍(如阀门、弯头、变截面管等)时,由于水流变形、方向变化、速度重新分布,质点间进行剧烈动量交换而产生的阻力。 6. 有旋流动、无旋流动 有旋流动:流体微团的旋转角速度不等于零的流动称为有旋流动。 无旋流动:流体微团的旋转角速度等于零的流动称为无旋流动。 试 题: 班号: 姓名: 第 2 页 (共 6 页) 二. 推求流线的微分方程(1 0 分) sd0d和vsv方向相同 某瞬时在流线上任取一点),,(zyxM,位于M 点的流体质点速度为v ,其分量为zyxvvv,,,在流线上取无穷小线段sd ,其在三个坐标轴上的投影为 dzdydx,,,由空间几何关系及有sd和v方向相同: dsdzzsdzvvvdsdyysdyvvvdsdxxsdxvvvzyx),cos(),cos(),cos(),cos(),cos(),cos(vdsvdzvdyvdxzyx(流线微分方程) 三. 推求流体静平衡微分方程(1 0 分) 在静止流体中取如图所示微小六面体。 设其中心点),,(zyxA的密度为 ,压强为p ,所受质量力为f 。 由于压强分布是空间坐标的连续函数:),,(zyxpp ,那么cb,点上的静压强为: 2dxxpppb 2dxxpppc (泰勒级数展开,略去小项) 以 X 方向为例,列力平衡方程式: 表面力: dxdydzxpdydzpdydzpcb 质量力:ρdxdydzfx 根据 ,0xF有 0dxdydzxpdxdydzρfx 01xpfx ...