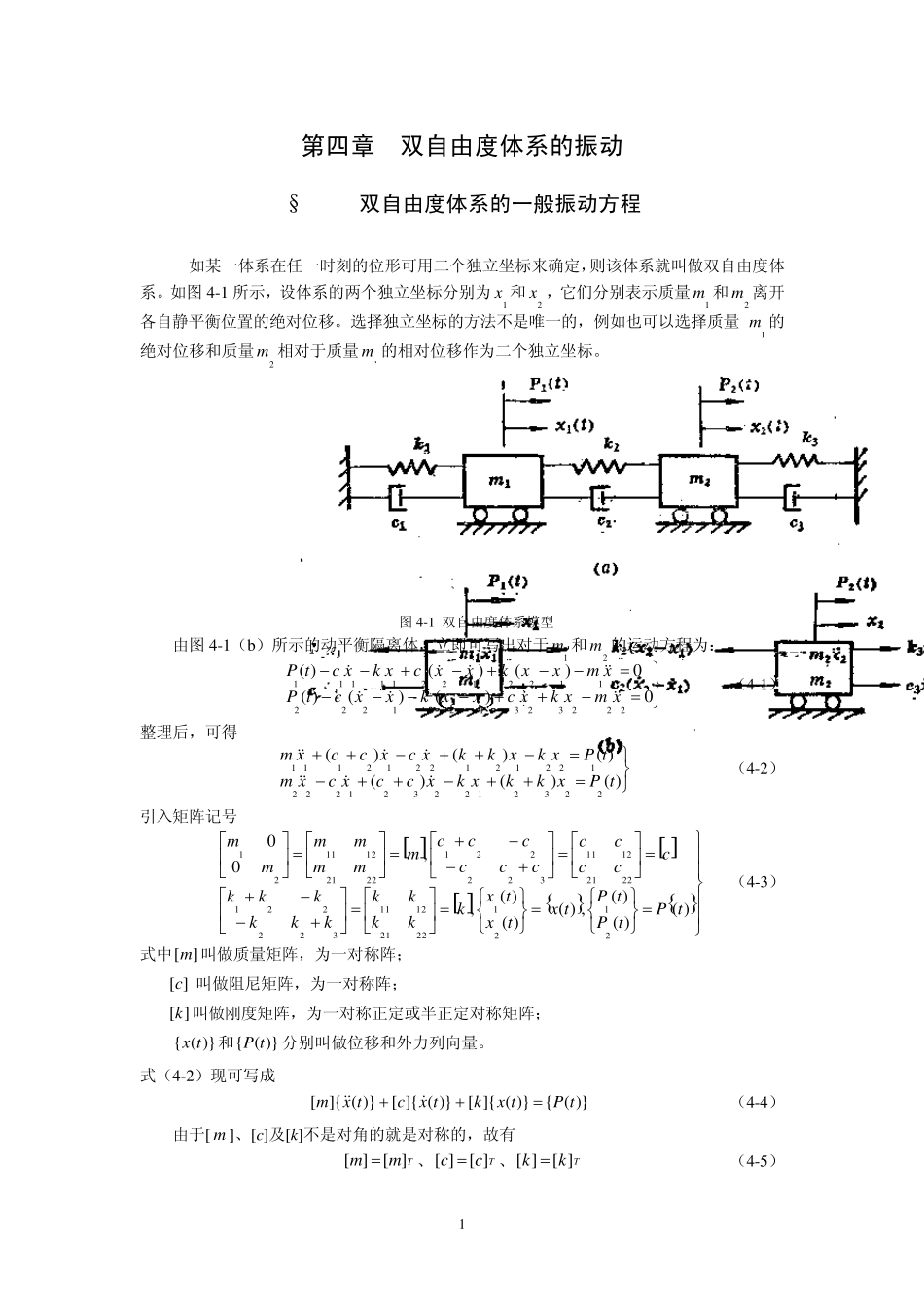
1 第四章 双自由度体系的振动 §4-1 双自由度体系的一般振动方程 如某一体系在任一时刻的位形可用二个独立坐标来确定,则该体系就叫做双自由度体系。如图4-1 所示,设体系的两个独立坐标分别为1x 和2x ,它们分别表示质量1m 和2m 离开各自静平衡位置的绝对位移。选择独立坐标的方法不是唯一的,例如也可以选择质量1m 的绝对位移和质量2m 相对于质量1m 的相对位移作为二个独立坐标。 图4-1 双自由度体系模型 由图4-1(b)所示的动平衡隔离体,立即可写出对于1m 和2m 的运动方程为: 0)()()(0)()()(22232312212221112212211111xmxkxcxxkxxctPxmxxkxxcxkxctP (4-1) 整理后,可得 )()()()()()(22321223212221221212212111tPxkkxkxccxcxmtPxkxkkxcxccxm (4-2) 引入矩阵记号 )()()(,)()()(,,00212122211211322221222112113222212221121121tPtPtPtxtxtxkkkkkkkkkkkcccccccccccmmmmmmm (4-3) 式中][m 叫做质量矩阵,为一对称阵; ][c 叫做阻尼矩阵,为一对称阵; ][k 叫做刚度矩阵,为一对称正定或半正定对称矩阵; )}({tx和)}({tP分别叫做位移和外力列向量。 式(4-2)现可写成 )}({)}(]{[)}(]{[)}(]{[tPtxktxctxm (4-4) 由于[ m ]、[c]及[k]不是对角的就是对称的,故有 Tmm][][、Tcc][][、Tkk][][ (4-5) 2 矩阵中的非对角元素起了耦合的作用。如果[ m ]、[c]及[k]均为对角阵时,则方程(4-4)解耦,此时其求解方法与单自由度体系相同。这个结论对一般多自由度体系也同样适用。 §4-2 双自由度体系的无阻尼振动 4-2-1 无阻尼时的运动方程 把式(4-4)中的阻尼项去掉,即令[c]=[0],即可得无阻尼时的运动方程 )}({}]{[)}(]{[tPxktxm (4-6) 在一般情况下,求解式(4-4)或上式也并不是很容易的,其原因是二个方程不是相互独立。下面我们仅讨论自由振动以及外力为简谐力的特殊情况。 4-2-2 自由振动 令式(4-6)的右侧}0{)({tP,即得自由振动方程式 }0{)}(]{[)}(]{[txktxm (4-7a) 上式也可写成 0212111212111xkxkxmxm 02221...