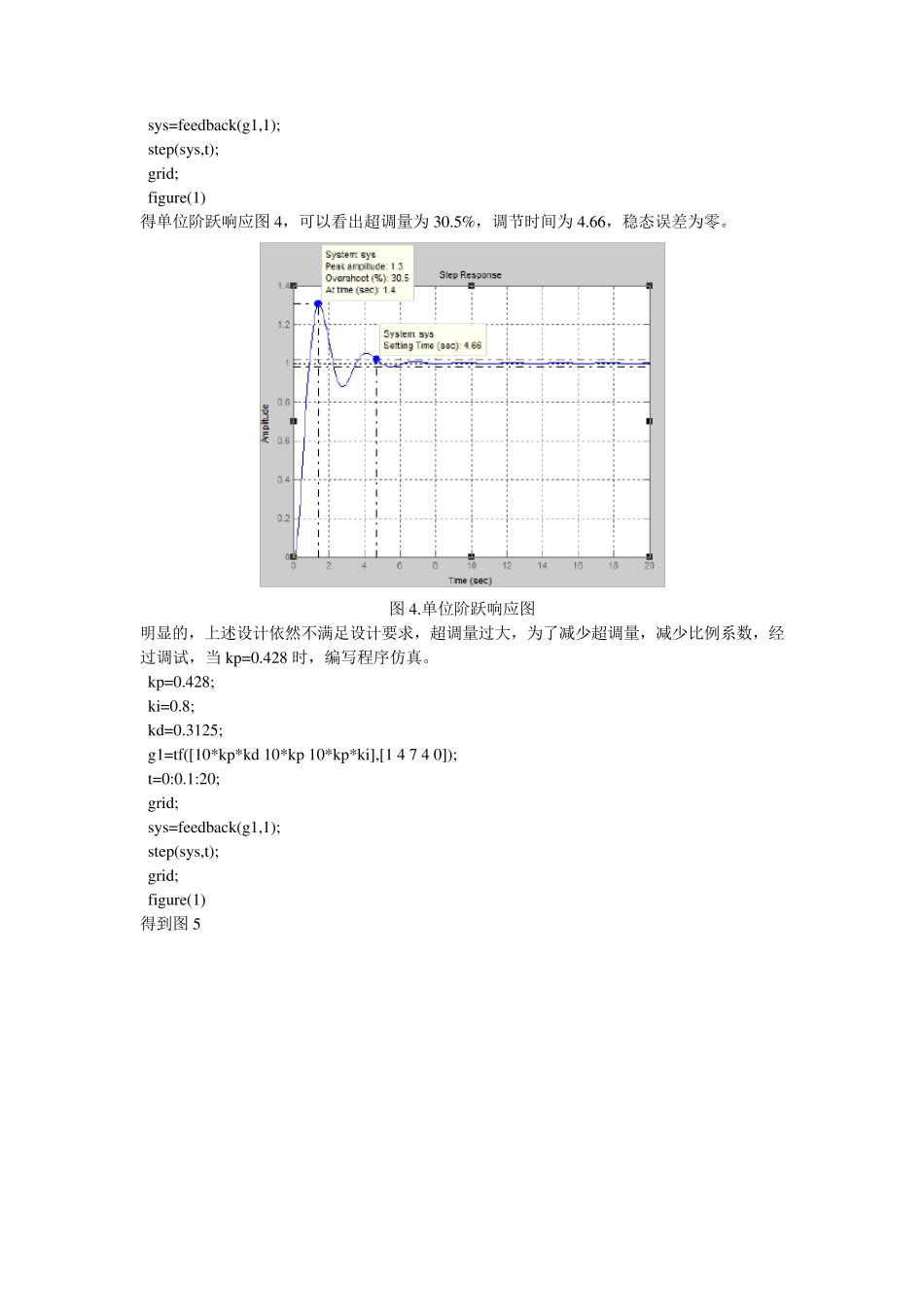
1.原控制系统的仿真 原被控对象传递函数为 )4S3S)(1(10)(2 SsG (1) 在matlab 中对原系统进行仿真,可得到其在单位阶跃输入的条件下的响应。 clear; nu m=10; den=conv ([1 1],[1 3 4]); g1=tf(nu m,den); t=0:0.1:20; sy s=feedback(g1,1); step(sy s,t); grid; figu re(1) 所得单位阶跃响应如图一所示,由图中可以看出此系统的超调量为43.2%,调节时间为8.45s,并且存在比较大的稳态误差. 图一 原系统单位阶跃响应 2.利用 P ID 算法改进系统性能 设计一个 PID 控制,使得超调量小于 10%,调节时间小于 3s,单位阶跃输入下的稳态误差为0.加入PID 控制器后系统的传递函数为 SSSSKiKpSKpSKdKpsG474*10*10**10)(2342 (2) 采用临界比例度法整定调节参数,此法是先求临界比例度 δk 和临界周期 Tk,根据经验关系求出各参数。先把积分时间调至iT = ,微分时间dT =0,调节器只利用纯比例作用。在干扰作用下整定比例度,使被调参数产生振荡,调到等幅振荡为止,记下这时的临界比例k 值,及临界 周期KT 值,根据经验计算各参数的整定值。 经验关系: PI 控制时:kikTT85.02.2 (3) PID 控制时:kdkikTTTT125.05.07.1 (4) 在SIMULINK 中搭建如图 2 模型,通过调整比例参数,当比例系数为2.38 时,产生等幅振荡,如图 3 所示。 图 2.改进后的结构图 图 3.单位阶跃响应图 用临界比例度法,根据图 3 得k =2.38,KT =2.5,代入公式 4 中得 kp=1.428,ki=0.8,kd=0.3125 代入公式 2 中编程,如下: clear kp=1.428; ki=0.8; kd=0.3125; g1=tf([10*kp*kd 10*kp 10*kp*ki],[1 4 7 4 0]); t=0:0.1:20; sy s=feedback(g1,1); step(sy s,t); grid; figu re(1) 得单位阶跃响应图4,可以看出超调量为30.5%,调节时间为4.66,稳态误差为零。 图4.单位阶跃响应图 明显的,上述设计依然不满足设计要求,超调量过大,为了减少超调量,减少比例系数,经过调试,当 kp=0.428 时,编写程序仿真。 kp=0.428; ki=0.8; kd=0.3125; g1=tf([10*kp*kd 10*kp 10*kp*ki],[1 4 7 4 0]); t=0:0.1:20; grid; sy s=feedback(g1,1); step(sy s,t); grid; figu re(1) 得到图5 图5.单位阶跃响应 由图5 可得,超调量为1.25%,调节时间为2.58,稳态误差为0,满足设计要求。 编写程序得到根轨迹图6 和伯德图7. clear kp=0.428; ki=0.8; kd=0.3125; g1=tf([10*kp*kd 10*kp 10*kp*ki],[1 4 7 4 0]); t=0:0.1:20; bode(g1); figu re(1) rlocu s(g1); figu re(2) rlocu s(g1) 图6.根轨迹图 图7 .伯德图 3 在系统稳定后加入干扰,如图8 所示。 . 图8 .加干扰的系统结构图 示波器的波形如图9 所示。 图9 .加扰动的单位阶跃响应图 由上图可知,在稳定后加入干扰,系统会出现波动,但马上又恢复到稳态,说明此系统具有一定的抗干扰能力。