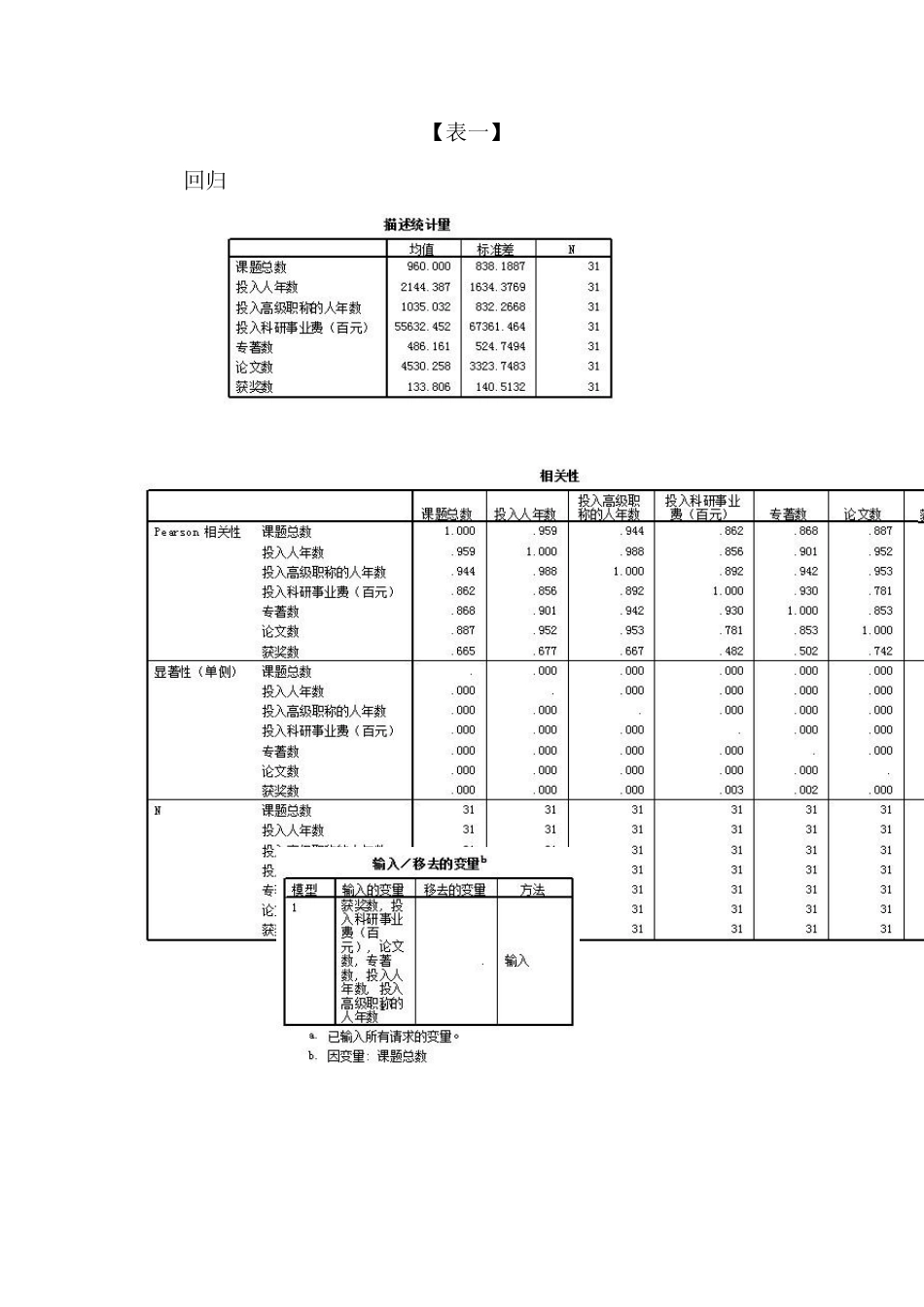
实验二 多重回归分析 一、实验目的 研究样本数据离差阵、样本协方差阵,以及变量之间的相关系数(包括偏相关)并作相关性分析。 二、实验要求 为研究高等院校人文社会科学研究中立项课题数受那些因素的影响,收集到某年31 个地区部分高校有关社科研究方面的数据(见SPSS 数据),利用此的数据,设定立项课题数X 5 为因变量(被解释变量),X 2,X 3,X 4,X 6,X 7,X 8 为解释变量,作多重回归分析。 三、实验内容 1.依次点击“分析→回归→线性回归”,得到如下图一所示: 【图一】 2.点击“统计量”,得到如下图二所示: 【图二】 3.点击“继续”,得到如下图三所示: 【图三】 4.点击“继续→确定”,得到如下表一所示: 【表一】 回归 其中,容差(容忍度):21iiTo lR 2iR 是解释变量iX 与其他解释变量间的复相关系数的平方。容忍度取值范围为 0-1,越接近 0表示多重共线性越强,容忍度越接近于 1表示多重共线性越弱。 方差膨胀因子(VIF): 1iiVIFTol即为容忍度的倒数。iVIF 的值大于等于 1,iVIF 越小,说明多重共线性越弱。 可见,投入高级职称的人年数的容差最小,为 0.007,多重共线性是最弱的,其次是投入人年数;获奖数的容差最大,为 0.358,多重共线性最强。 其中,解释变量相关阵的特征根和方差比:如果解释变量有较强的相关性,则它们之间必然存在信息重叠。可通过解释变量相关阵的特征值来反映。解释变量相关阵的最大特征根能够解释说明解释变量信息的比例是最高的,其他特征根随其特征值的减小对解释变量方差的的解释能力依次减弱。如果这些特征根中,最大特征根远远大于其他特征根,说明这些解释变量间具有相当多的重叠信息。 条件指数:是在特征值基础上的定义的能反映解释变量间多重共线性的指标 miik ik 为第i个条件指数,m 是最大特征根。 通常当010ik时,认为多重共线性弱;当10100ik时,认为多重共线性较强;当是100ik ,认为多重共线性很严重。 可见,专著数、论文数及获奖数的多重共线性较强;投入人年数、投入高级职称的人年数及投入科研事业费的多重共线性较弱。 通过观察数据窗口的库克距离和杠杆值变量的值,发现没有明显的异常点。 综上分析,因此此模型需要改进。 将方法中的 “进入”改为“逐步”,其余操作不变,如下图四所示: 【图四】 点击“确定”,得到如表二所示: 【表二】 回归 可见,投入高级职称的人年数的...