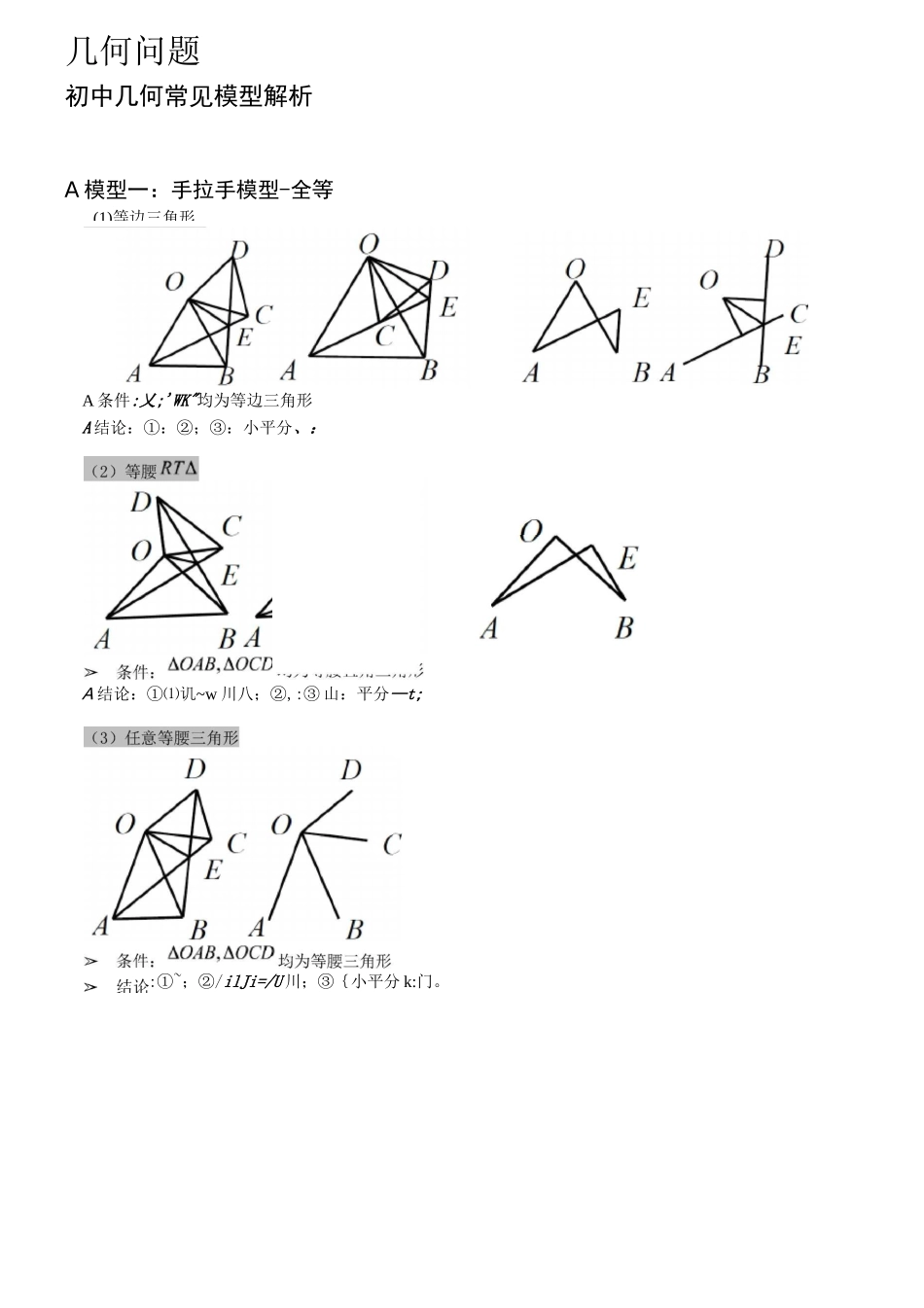
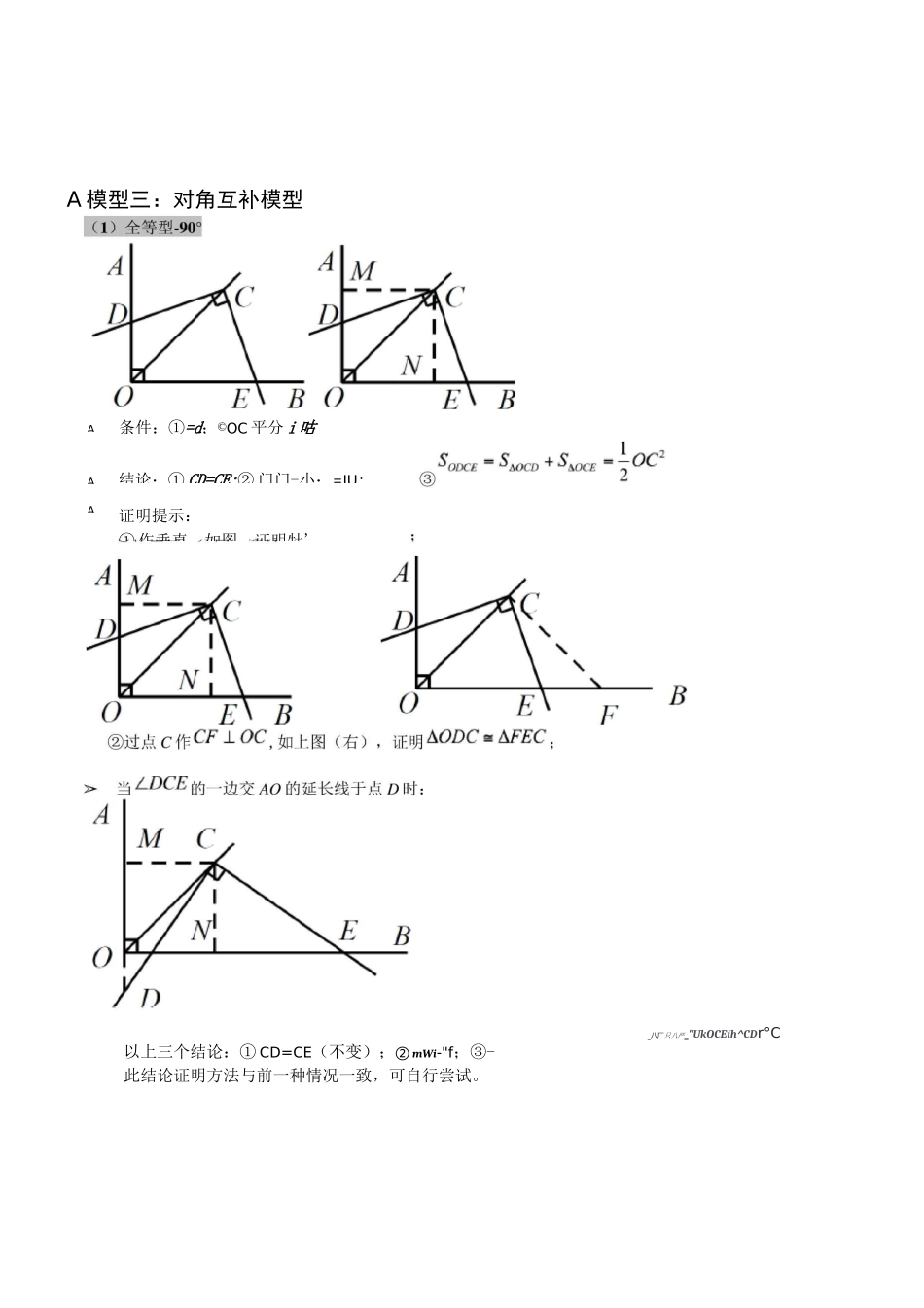
几何问题初中几何常见模型解析A 模型一:手拉手模型-全等A 条件:乂;'WK"均为等边三角形A 结论:①:②;③:小平分、:(1)等边三角形A 结论:①⑴讥~w 川八;②,:③ 山:平分—t;:①~;②/ilJi=/U 川;③{小平分 k:门。BDOP0B~AC~OC~~OAtanLOC⑤ 连接 AD、BC,必有A 模型二:手拉手模型-相似(1)A条件:'门川,将旋转至右图位置A结论:右图中①■'■;② 延长 AC 交 BD 于点 E,必有A条件:5 川,,将心八旋转至右图位置A 结论:右图中①■'';②延长 AC 交 BD 于点 E,必有门“汎R+.舷_.冶_[门;9⑥'V5"(对角线互相垂直的四边形)(2)特殊情A 模型三:对角互补模型_八厂只八严_"UkOCEih^CDr°C以上三个结论:① CD=CE(不变);② mWi-"f;③-此结论证明方法与前一种情况一致,可自行尝试。条件:①=d;©OC 平分 i 咕AAA结论:① CD=CE;② 门门-小:=JU;证明提示:① 作垂直,如图,证明牡'条件:①结论:①V=V+V结论:①;②:③证明提示:①可参考“全等型-90°”证法一;②如图:在 OB 上取一点 F,使 OF=OC,证明乜妊八为等边三角形。当的一边交 AO 的延长线于点 D 时(如上图右):原结论变成:①②_______________________________③_______________________________可参考上述第②种方法进行证明。(3)全等型-任意角“:②〔•刀三〔E;平分;② dm;OC1*$ina*cosa当的一边交 AO 的延长线于点 D 时(如右上图):原结论变成:①②③可参考上述第②种方法进行证明。◊请思考初始条件的变化对模型的影响。:② 门「平分 m;£广 F结论:①"=② 汕—丸V+V=V巳 XE 丁 2 加卫 F—7 生 OCT且 s^r=^oc'^na竺二僅二空“哑(关键步)DOCDCO结论③得二 KDCMKEF二 ZCDO=ZCEF二 ZCZX7+ZCW=J80°TZ^^+ZZX£=180°ZDCO=ZECF结论②得*:^I)CE=ZOCF=90aV(OE+EF)*cosa=OC证明::.EF=6ZZ>taiia结论①得证如图所示,若将条件 w 平分川”去掉,条件①不变,皿平分/5,结论变化如下:OBEOOBBEEMDDAAA 对角互补模型总结:① 常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线;② 初始条件“角平分线”与“两边相等”的区别;③ 两种常见的辅助线作法;④ 注意下图中’平分时,八门上―门=/X 门二‘f 门相等是如何推导的?A 模型四:角含半角模型 90。(2)角含半角模型 90°-2LEAF=45°结论:A结论:A辅助线如下图所示:条件:①正方形;② 一亠结论:①上 m 处;②...