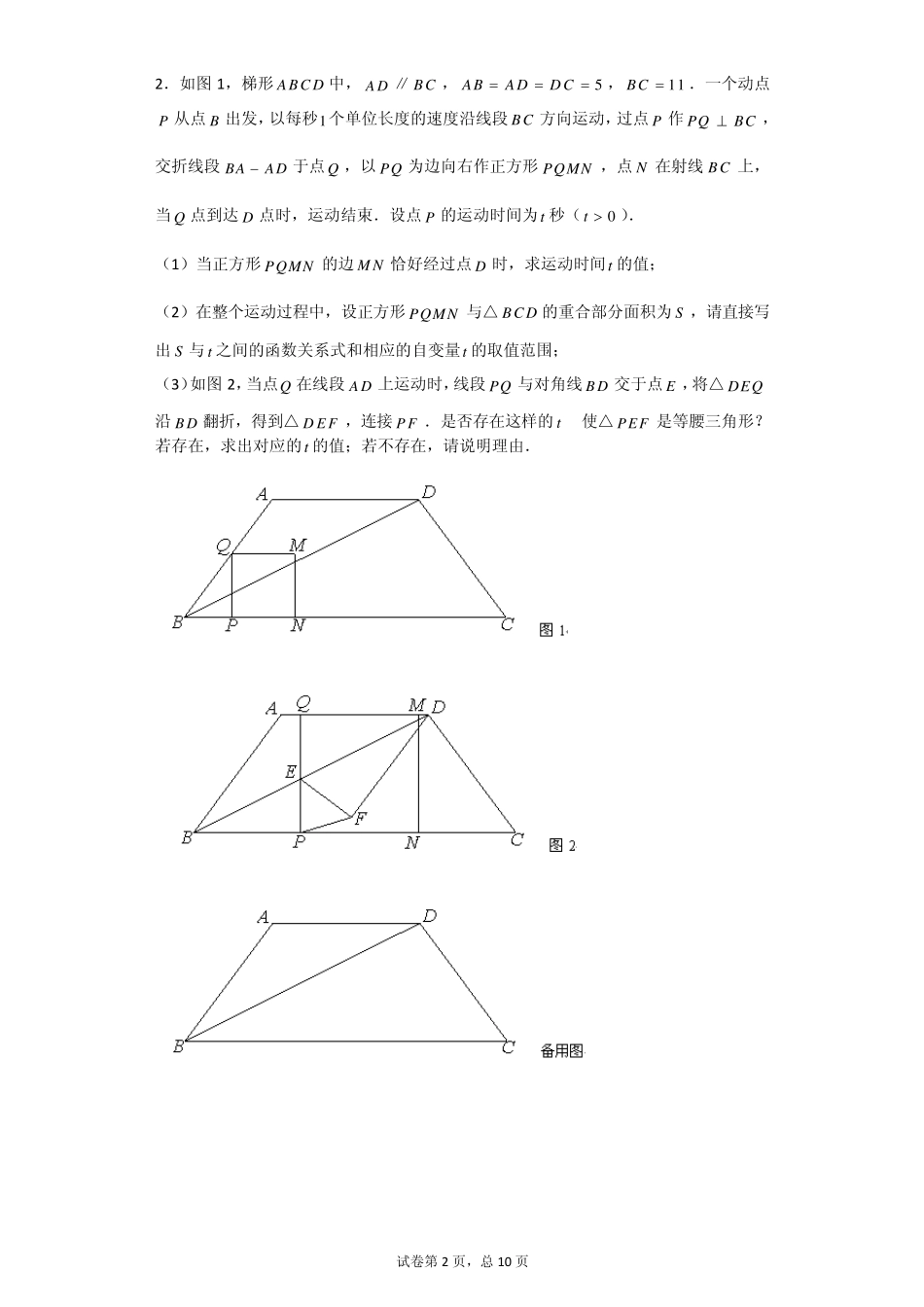
试卷第1 页,总10 页 二次函数中寻找等腰三角形问题 1.如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=32,直线y=323x经过点C,交y轴于点G,且∠AGO=30°。 (1)点C、D的坐标 (2)求顶点在直线y=323x上且经过点C、D的抛物线的解析式; (3)将(2)中的抛物线沿直线y=323x平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。 试卷第2 页,总10 页 2.如图1,梯形ABC D 中,A D ∥ BC ,5ABADDC,11BC .一个动点P 从点 B 出发,以每秒1个单位长度的速度沿线段 BC 方向运动,过点 P 作 PQBC,交折线段 BAAD于点 Q ,以 PQ 为边向右作正方形PQMN ,点 N 在射线 BC 上,当 Q 点到达 D 点时,运动结束.设点 P 的运动时间为t秒(0t ). (1)当正方形PQMN 的边 M N 恰好经过点 D 时,求运动时间t的值; (2)在整个运动过程中,设正方形PQMN 与△ BC D 的重合部分面积为 S ,请直接写 出 S 与 t之间的函数关系式和相应的自变量t的取值范围; (3)如图2,当点Q 在线段 A D 上运动时,线段 PQ 与对角线 B D 交于点 E ,将△ DEQ 沿 B D 翻折,得到△ D E F ,连接 P F .是否存在这样的 t ,使△ PEF 是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由. 试卷第3 页,总10 页 3.已知两直线l1,l2分别经过点A(1,0),点B(-3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示. (1)求点C的坐标,并求出抛物线的函数解析式; (2)抛物线的对称轴被直线l1、抛物线、直线l2和 x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由; (3)当直线l2绕点C旋转时,与抛物线的另一个交点为 M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标: 试卷第4 页,总10 页 4.如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P 为二次函数图象上的一个动点,过点P 作x轴的垂线,垂足为D(m,0),并与直线OA交于点C. (1)求出二次函数的解析式; (2)当点P 在直线OA的上方时,用含m的代数式表示线段PC 的长,并求线段PC 的最大值; (3)当m>0时,探索是否存在点P,使得△PCO 为...