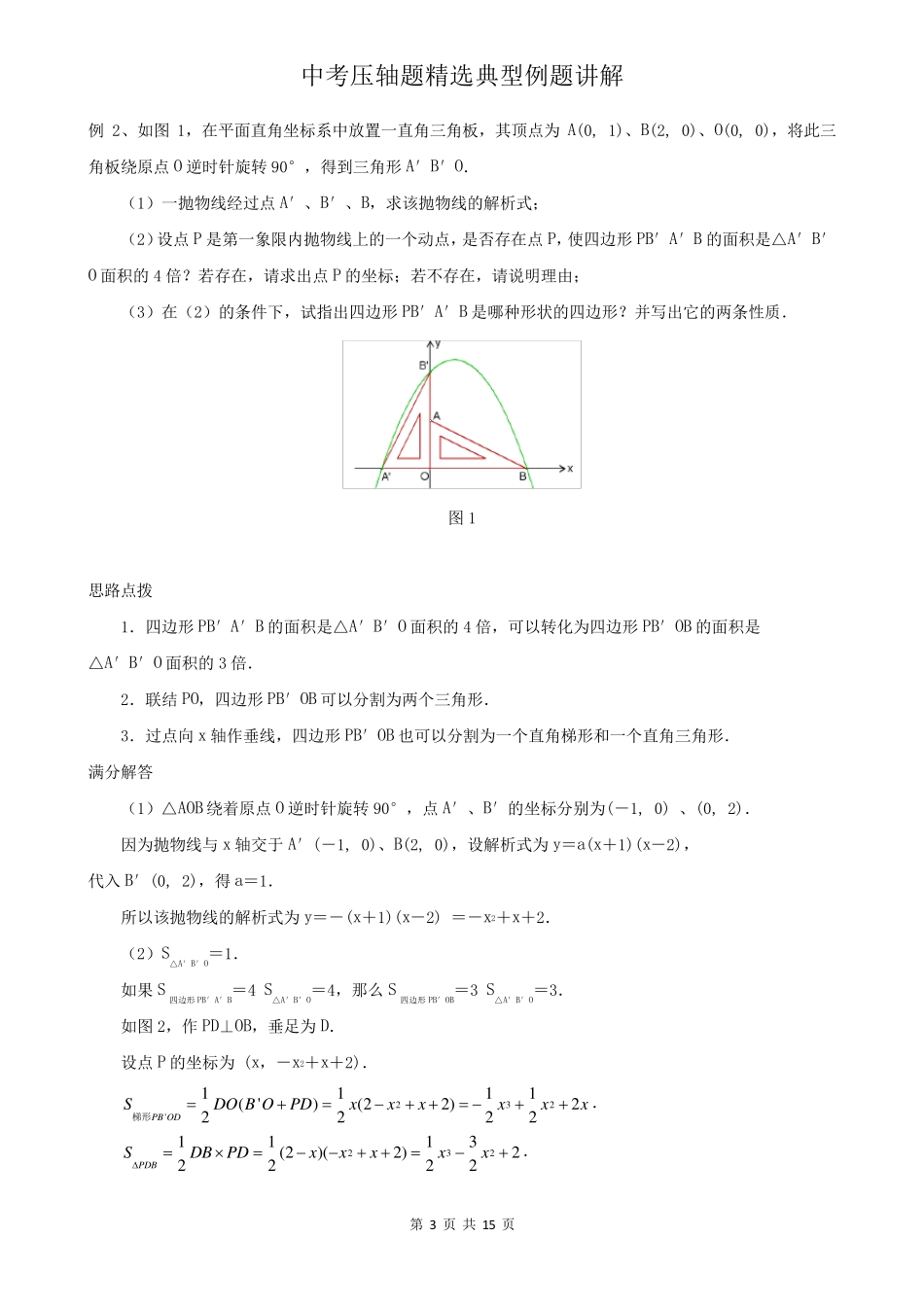
中考压轴题精选典型例题讲解 第 1 页 共 15 页 二次函数-因动点产生的面积问题 例1、如图1,已知抛物线 212yxbxc(b、c 是常数,且c<0)与x 轴交于A、B 两点(点A 在点B的左侧),与y 轴的负半轴交于点C,点A 的坐标为(-1,0). (1)b=______,点B 的横坐标为_______(上述结果均用含c 的代数式表示); (2)连结BC,过点A 作直线AE//BC,与抛物线交于点E.点D 是x 轴上一点,坐标为(2,0),当C、D、E 三点在同一直线上时,求抛物线的解析式; (3)在(2)的条件下,点P 是x 轴下方的抛物线上的一动点,连结PB、PC.设△PBC 的面积为S. ①求S 的取值范围; ②若△PBC 的面积S 为正整数,则这样的△PBC 共有_____个. 图1 思路点拨 1.用c 表示b 以后,把抛物线的一般式改写为两点式,会发现OB=2OC. 2.当C、D、E 三点共线时,△EHA∽△COB,△EHD∽△COD. 3.求△PBC 面积的取值范围,要分两种情况计算,P 在BC 上方或下方. 4.求得了 S 的取值范围,然后罗列 P 从 A 经过C 运动到 B 的过程中,面积的正整数值,再数一数个数.注意排除点A、C、B 三个时刻的值. 满分解答 (1)b=12c,点B 的横坐标为-2c. (2)由2111()(1 )(2 )222yxcxcxxc,设E1( ,(1 )(2 ))2xxxc. 过点E 作EH⊥x 轴于H. 由于OB=2OC,当AE//BC 时,AH=2EH. 所以1(1 )(2 )xxxc .因此12xc .所以(12 ,1)Ecc. 中考压轴题精选典型例题讲解 第 2 页 共 15 页 当C、D、E 三点在同一直线上时,EHCODHDO.所以1212ccc. 整理,得2c2+3c-2=0.解得c=-2 或12c (舍去). 所以抛物线的解析式为 213222yxx. (3)①当P 在BC 下方时,过点P 作 x 轴的垂线交 BC 于 F. 直线BC 的解析式为122yx. 设213( ,2 )22P mmm,那么1( ,2 )2F mm ,2122FPmm . 所以S△PBC=S△PBF+S△PCF=221()24(2 )42BCFP xxFPmmm . 因此当P 在BC 下方时,△PBC 的最大值为4. 当P 在BC 上方时,因为S△ABC=5,所以S△PBC<5. 综上所述,0<S<5. ②若△PBC 的面积 S 为正整数,则这样的△PBC 共有 11 个. 考点伸展 点P 沿抛物线从 A 经过 C 到达 B 的过程中,△PBC 的面积为整数,依次为(5),4,3,2,1,(0),1,2,3,4,3...