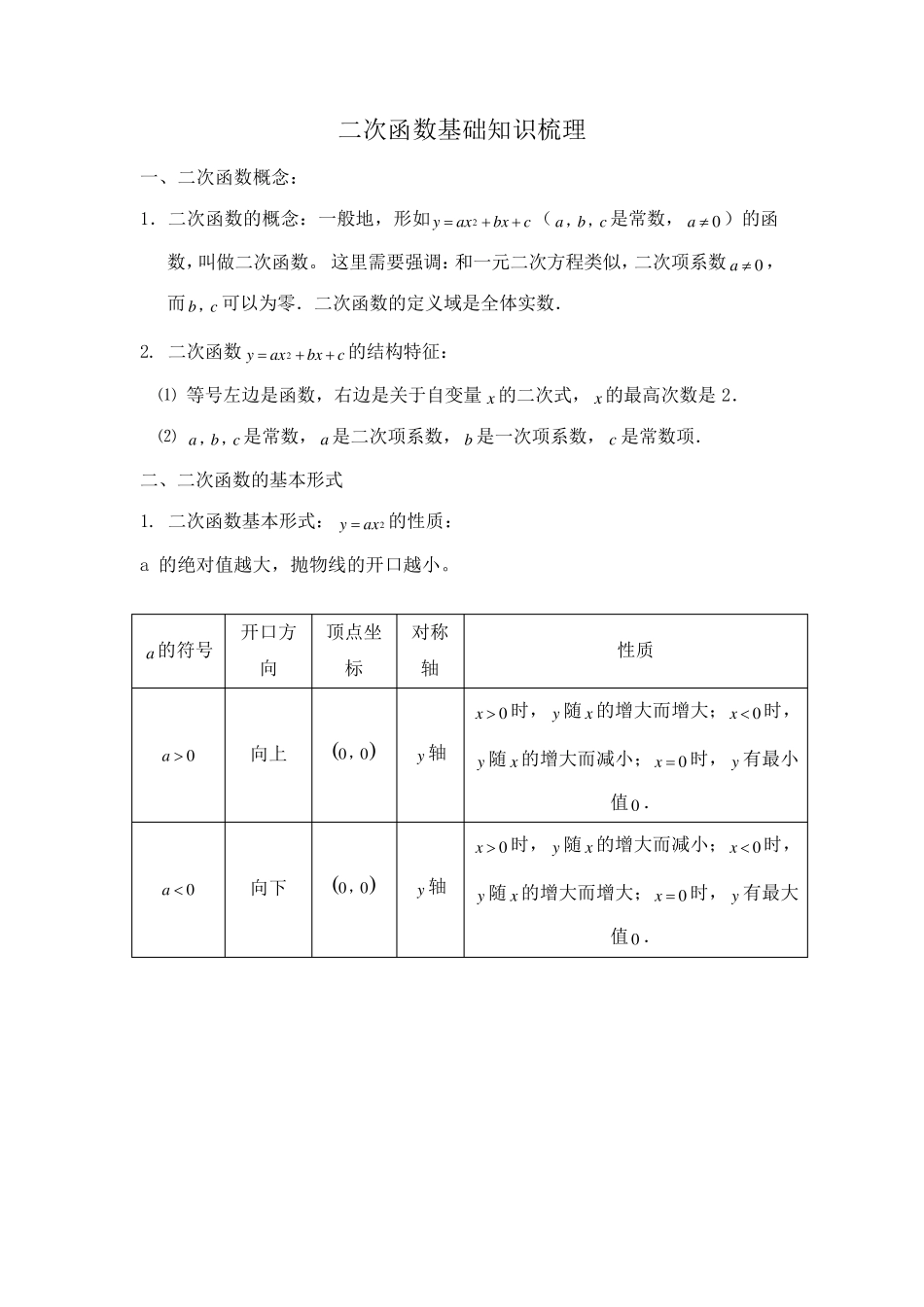
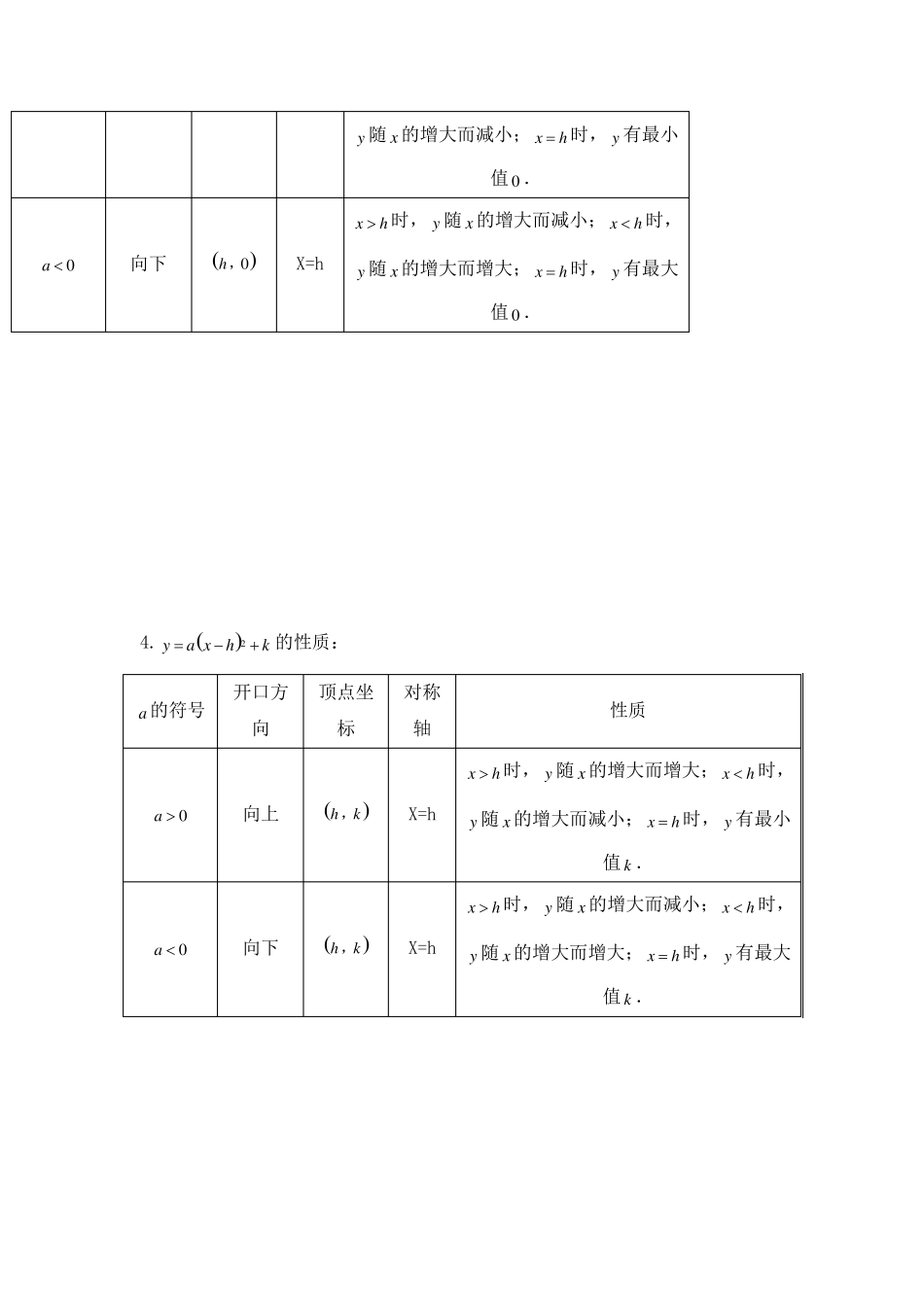
二次函数基础知识梳理 一、二次函数概念: 1.二次函数的概念:一般地,形如2yaxbxc (abc, , 是常数,0a )的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数0a ,而bc, 可以为零.二次函数的定义域是全体实数. 2. 二次函数2yaxbxc 的结构特征: ⑴ 等号左边是函数,右边是关于自变量 x的二次式,x的最高次数是2. ⑵ abc, , 是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式 1. 二次函数基本形式:2yax的性质: a 的绝对值越大,抛物线的开口越小。 a 的符号 开口方向 顶点坐标 对称轴 性质 0a 向上 00, y轴 0x 时,y 随 x的增大而增大;0x时,y随 x的增大而减小;0x 时,y 有最小值 0 . 0a 向下 00, y轴 0x 时,y 随 x的增大而减小;0x时,y随 x的增大而增大;0x 时,y 有最大值 0 . 2. 2yaxc 的性质: 上加下减。 3. 2ya xh的性质: 左加右减。 a 的符号 开口方向 顶点坐标 对称轴 性质 0a 向上 0c, y轴 0x 时, y随 x的增大而增大;0x 时,y随 x的增大而减小;0x 时, y 有最小值 c . 0a 向下 0c, y轴 0x 时, y随 x的增大而减小;0x 时,y随 x的增大而增大;0x 时, y 有最大值 c . a 的符号 开口方向 顶点坐标 对称轴 性质 0a 向上 0h, X=h xh 时, y随 x的增大而增大; xh时, 4.2ya xhk的性质: y随x的增大而减小;xh时,y 有最小值0 . 0a 向下 0h, X=h xh时,y随x的增大而减小;xh时,y随x的增大而增大;xh时,y 有最大值0 . a 的符号 开口方向 顶点坐标 对称轴 性质 0a 向上 hk, X=h xh时,y 随x的增大而增大;xh时,y随x的增大而减小;xh时,y 有最小值k . 0a 向下 hk, X=h xh时,y 随x的增大而减小;xh时,y随x的增大而增大;xh时,y 有最大值k . 三、二次函数图象的平移 1. 平移步骤: 方法一:⑴ 将抛物线解析式转化成顶点式2ya xhk,确定其顶点坐标hk, ; ⑵ 保持抛物线2yax的形状不变,将其顶点平移到hk, 处,具体平移方法如下: 2. 平移规律 在原有函数的基础上“h 值正右移,负左移...