二阶导数意义VIP免费

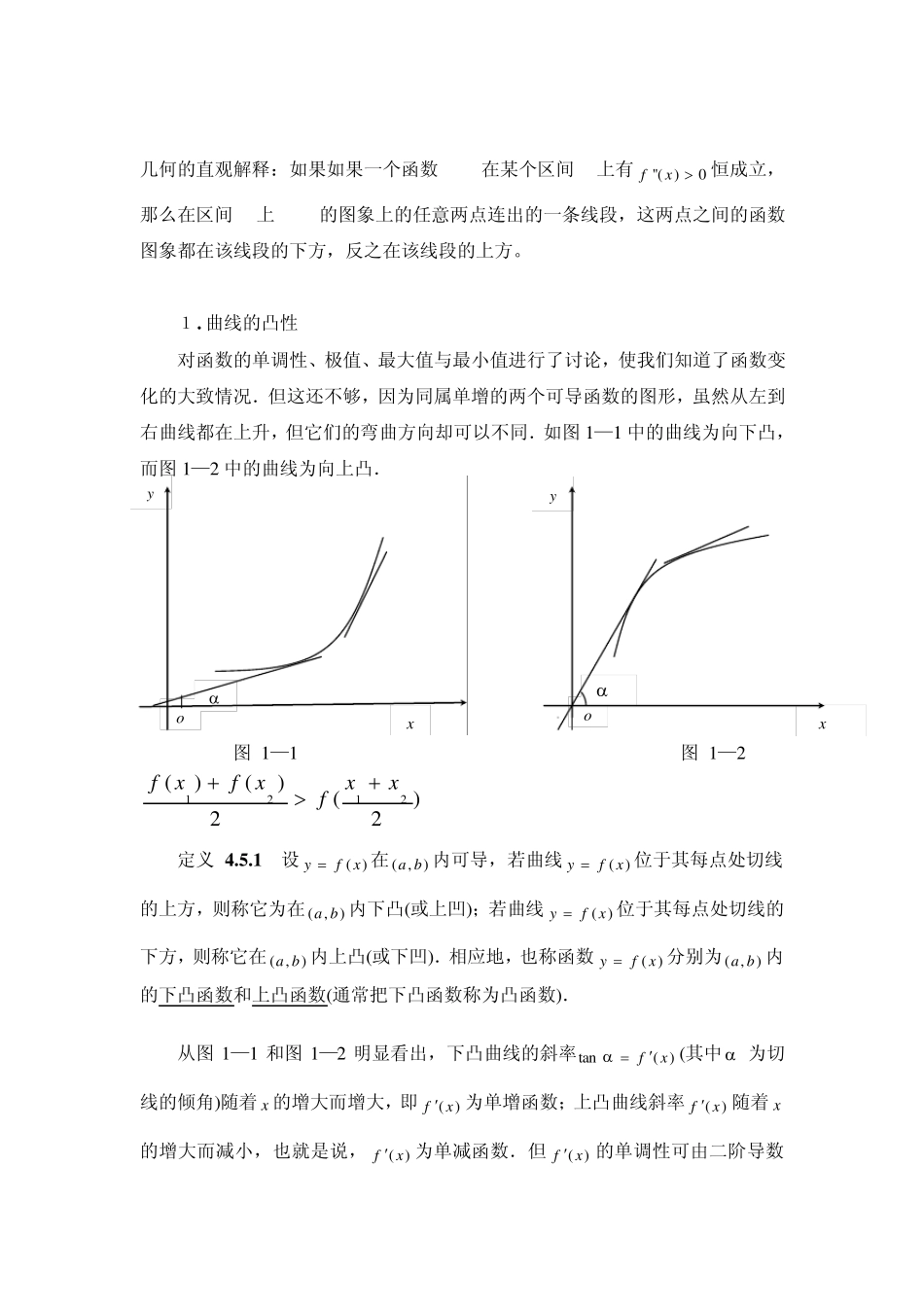
二阶导数的意义 二阶导数就是对一阶导数再求导一次， 意义如下： （1）斜线斜率变化的速度，表示的是一阶导数的变化率 （2）函数的凹凸性。 （3）判断极大值极小值。 结合一阶、二阶导数可以求函数的极值。当一阶导数等于零，而二阶导数大于零时，为极小值点；当一阶导数等于零，而二阶导数小于零时，为极大值点；当一阶导数、二阶导数都等于零时，为驻点。 一、用二阶导数判断极大值或极小值定理 设)( xf在0x二阶可导，且0)(,0)(00xfxf． (1 ) 若0)(0 xf，则)( xf在0x取得极大值； (2 ) 若0)(0 xf，则)( xf在0x 取得极小值． 例 试问a 为何值时，函数xxaxf3sin31sin)(在3x处取得极值？它是极大值还是极小值？求此极值． 解 xxaxf3c o sc o s)(． 由假设知0)3( f，从而有012a，即2a． 又当2a时，xxxf3sin3sin2)(，且 03)3( f，所以xxxf3sin31sin2)(在3x处取得极大值，且极大值3)3(f． 例 求函数593)(23xxxxf的极大值与极小值． 解 )( xf在]4,2[上连续，可导．令 0)3)(1(3963)(2xxxxxf， 得 1x和3x， 思考： )( xf在1x取得极大还是极小值？在3x取得极大还是极小值？ '( )66fxx -1 代入二阶导数表达式为-12，)( xf在1x取得极大值 3 代入二阶导数表达式12，在3x取得极小值 三、函数图像凹凸定理 若)( xf在),(ba内二阶可导， 则 曲 线)( xfy 在),(ba内 的图 像 是凹 曲 线 的充 要 条 件 是0)( xf，),(bax ． 曲 线)( xfy 在),(ba内 的图 像 是凸 曲 线 的充 要 条 件 是0)( xf，),(bax 。 o o x x y y 几何的直观解释：如果如果一个函数f(x)在某个区间I上有''( )0fx 恒成立，那么在区间I上f(x)的图象上的任意两点连出的一条线段，这两点之间的函数图象都在该线段的下方，反之在该线段的上方。 １. 曲线的凸性 对函数的单调性、极值、最大值与最小值进行了讨论，使我们知道了函数变化的大致情况．但这还不够，因为同属单增的两个可导函数的图形，虽然从左到右曲线都在上升，但它们的弯曲方向却可以不同．如图1—1 中的曲线为向下凸，而图1—2 中的曲线为向上凸． 图 1—1 图 1—2 1212()()()22fxfxxxf 定义 4 .5 .1 设)( xfy 在),(ba内可导，若曲线...