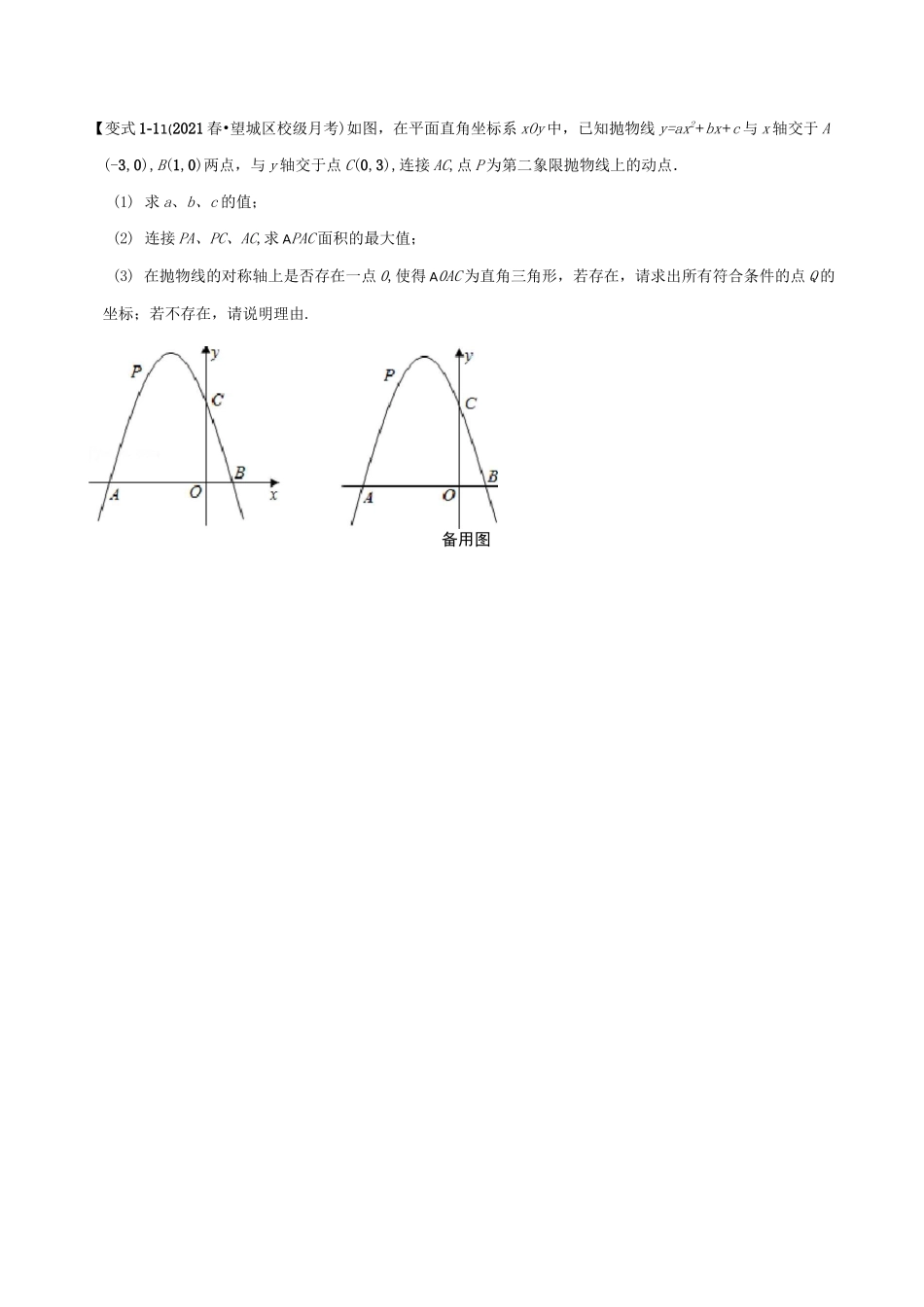
ysB團Aj_/OA/O点 P 是抛物线上一动点,连接 PB,PC.(D)点 A 的坐标为,点 B 的坐标为备用二次函数中的存沪科题型 1 二次函数中直角三角形存在性问题】亞型』H 函数中平行四迪出存隹性问題范型1 二双函前中白均三角弗殍在性麵型2 二之宙玆中轸腫三诙曲存在性題型6 二决硒戲中正方疋存在性範樂4 二谀函昨叢弗存在恒问題型5专题 21.10 二次函数中的存在性问题-重难点题型【例 D】(皿•罗湖区校级模拟)如图,已知抛物线 y=-^:DxDD 与 x 轴交于点 A、B,与 y 轴交于点 C,(D)如图 D,当点 P 在直线 BC 上方时,过点 P 作 PD 上 x 轴于点 D,交直线 BC 于点 E.若 PE=DED,求 APBC 的面积;(D)抛物线上存在一点 P,使 APBC 是以 BC 为直角边的直角三角形,求点 P 的坐标.【变式 1-11(2021 春•望城区校级月考)如图,在平面直角坐标系 xOy 中,已知抛物线 y=ax2+bx+c 与 x 轴交于 A(-3,0),B(1,0)两点,与 y 轴交于点 C(0,3),连接 AC,点 P 为第二象限抛物线上的动点.(1) 求 a、b、c 的值;(2) 连接 PA、PC、AC,求 APAC 面积的最大值;(3) 在抛物线的对称轴上是否存在一点 0,使得 A0AC 为直角三角形,若存在,请求出所有符合条件的点 Q 的坐标;若不存在,请说明理由.备用图【变式 1-2】(2021•长沙模拟)如图,抛物线 y=-x2+bx+c 与 x 轴相交于 A、B 两点,与 y 轴相交于点 C,且点 B 与点 C 的坐标分别为 B(3,0).C(0,3),点 M 是抛物线的顶点.点 P 为线段 MB 上一个动点,过点 P 作 PD 丄 x 轴于点D,若 OD=m.(1)求二次函数解析式;(2) 设 APCD 的面积为 S,试判断 S 有最大值或最小值?若有,求出其最值,若没有,请说明理由;(3) 在 MB 上是否存在点 P,使 APCD 为直角三角形?若存在,请写出点 P 的坐标;若不存在,请说【变式 1-3】(2021•长沙模拟)如图,抛物线 y=ax234+bx 过 A(4,0),B(1,3)两点,点 C、B 关于抛物线的对称轴对称,过点 B 作直线 BH 丄 x 轴,交 x 轴于点 H.2直接写出点 C 的坐标,并求出 AABC 的面积;3点 P 是抛物线上一动点,且位于第四象限,当 AABP 的面积为 6 时,求出点 P 的坐标;4若点 M 在直线 BH 上运动,点 N 在 x 轴上运动,是否存在以点 C、M、N 为顶点的三角形为等腰直角三角形?若存在,请直接写出此时点 M 的坐标,若不存在,请说明理由.题型 2 二次函...