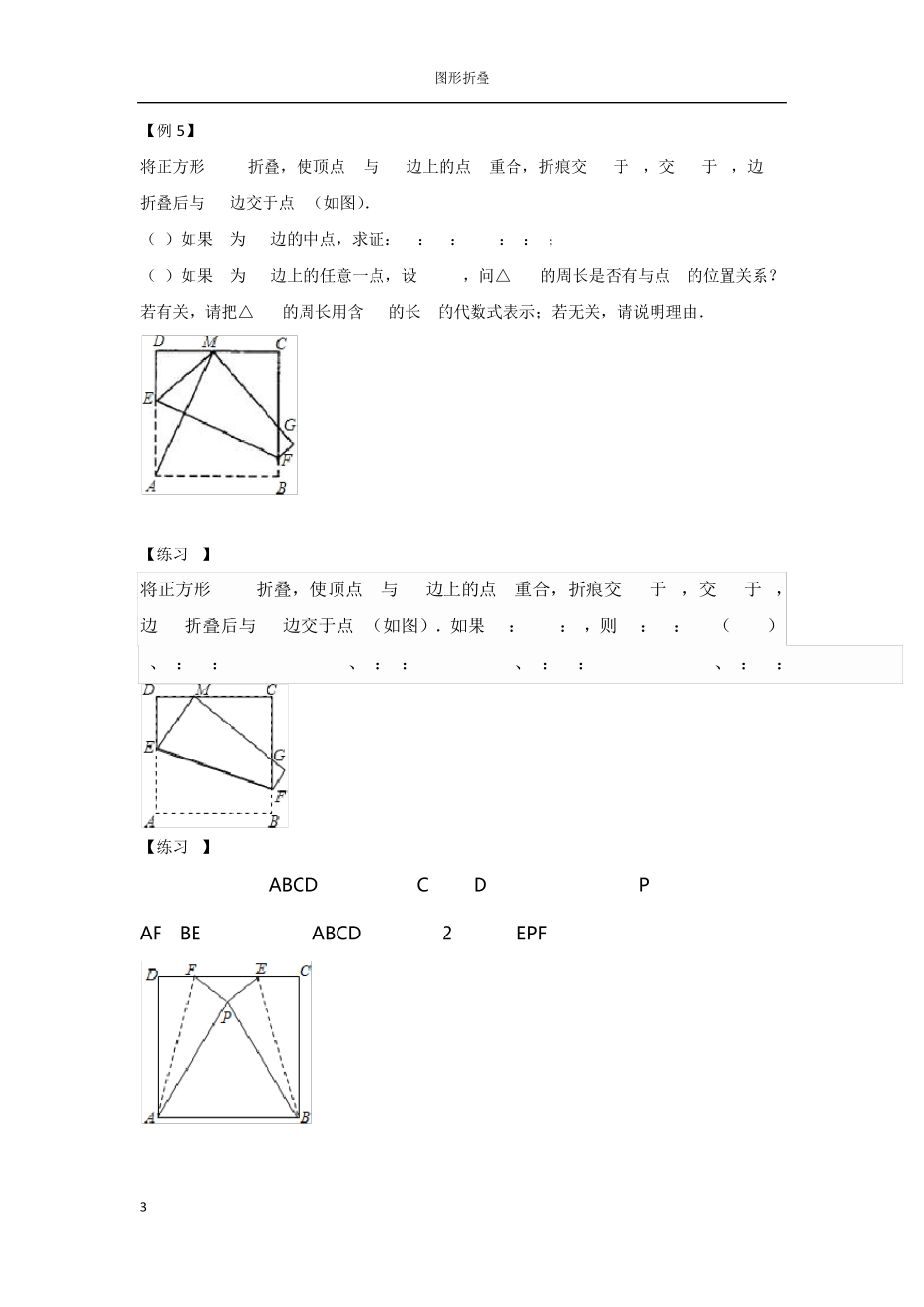
图形折叠 1 【例1】 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段 BF的取值范围为 3≤BF≤4;④当点H与点A重合时,EF=2.其中结论正确的个数是( ). A.1个 B.2个 C.3个 D.4个 【例2】 已知如图,长方形ABCD,AB=8,BC=6,若将长方形顶点A、C重合折叠起来,则折痕 PQ长为_________ 【例3】 如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5,在矩形ABCD的边AB上取一点M,在CD 上取一点N,将纸片沿MN折叠,使 MB与 DN交于点K,得到△MNK。 图形折叠 2 (1)若∠1=70°,求∠MKN的度数; (2)△MNK的面积能否小于?若能,求出此时∠1的度数;若不能,试说明理由; (3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,求最大值。 【例 4】 将一矩形纸片 OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点 Q 从点 O出发以每秒 1个单位长的速度沿 OC向终点 C运动,运动秒时,动点 P从点 A出发 以相等的速度沿 AO向终点 O运动,当其中一点到达终点时,另一点也停止运动.设点 P的 运动时间为 t(秒)。 (1)用含 t的代数式表示 OP=_______,OQ________; (2)当 t=1时,如图1,将沿△OPQ沿 PQ翻折,点 O恰好落在 CB边上的点 D处,求点 D的坐标; (3)连接 AC,将△OPQ沿 PQ翻折,得到△EPQ,如图2,问:PQ与 AC能否平行?PE与 AC能否垂直?若能,求出相应的 t值;若不能,说明理由。 图形折叠 3 【例5】 将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图). (1)如果M为CD边的中点,求证:DE:DM:EM=3:4:5; (2)如果M为CD边上的任意一点,设AB=2a,问△CMG的周长是否有与点M的位置关系?若有关,请把△CMG的周长用含 CM的长 x的代数式表示;若无关,请说明理由. 【练习 1】 将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).如果DM:MC=3:2,则 DE:DM:EM=( ) A、7:24:25 B、3:4:5 C、5:12:13 D、8:15:17 【练习 2】 如图,将正方形 ABCD 折叠,使点 C 与点 D 重合于正方形内点 P 处,折痕分别为AF、BE,如果正方形 ABCD 的边长是 2,那么△EPF ...