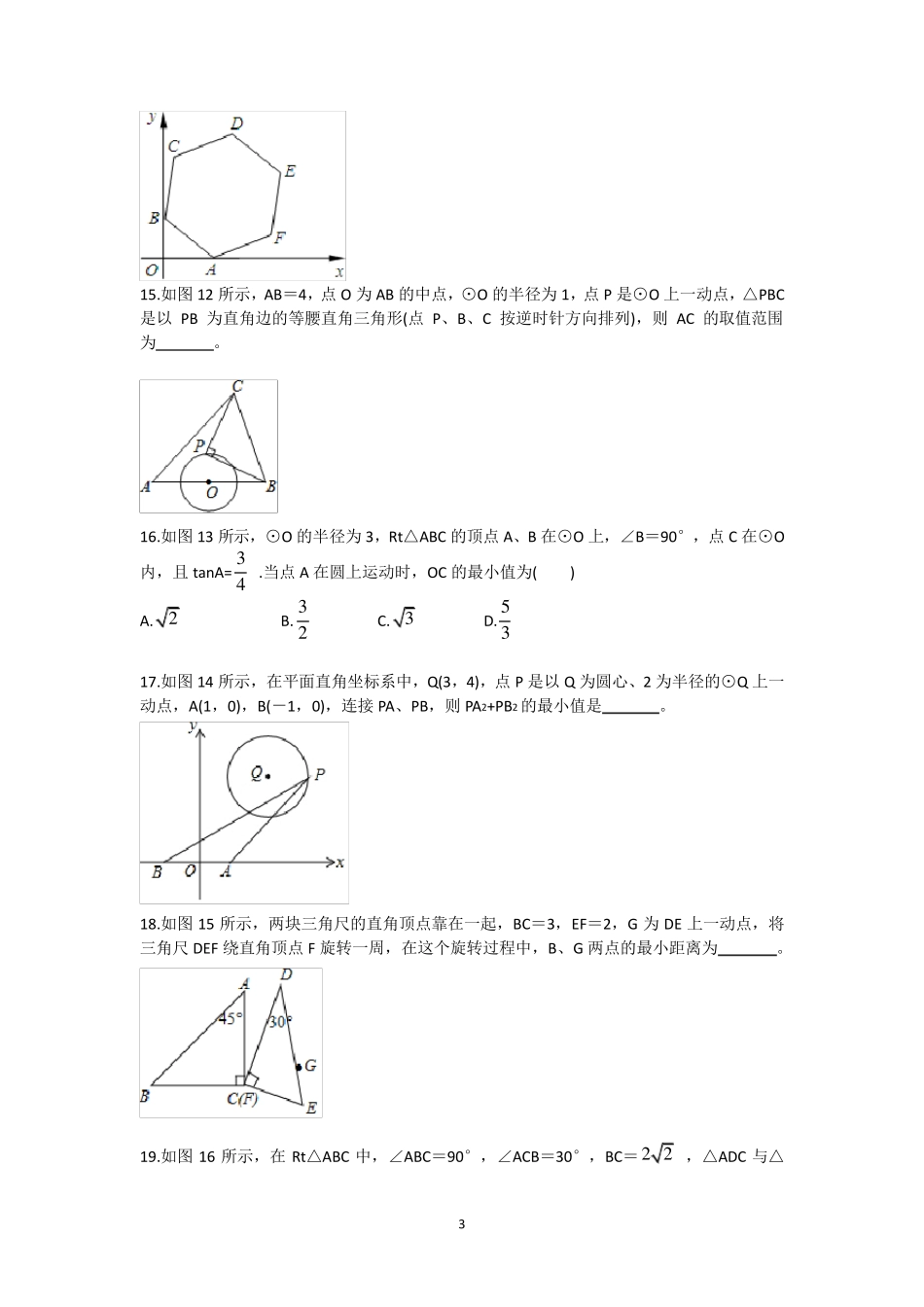
1 初中数学100 道经典最值题 1.如图1 所示,在Rt△ABC 中,∠A=30°,AB=4,D 为边 AB 的中点,P 为边 AC 上的动点,则 PB+PD 的最小值为( ) A. 3 B.2 2 C.2 3 D.4 5 2.如图2 所示,在矩形 ABCD 中,AB=5,AD=3,动点 P 满足13PABABCDSS矩形 ,则点 P到 AB 两点距离之和 PA+PB 的最小值为 。 3.如图3 所示,在矩形 ABCD 中,AD=3,点 E 为边 AB 上一点,AE=1,平面内动点 P 满足13PABABCDSS矩形,则|DP-EP|的最大值为 。 4.已知222222yxxxx ,则 y 的最小值为 。 5.已知223914yxx ,则 y 的最大值为 。 6.如图4 所示,在等腰 Rt△ABC 中,∠BAC=90°,AB=AC,BC=4 2 ,D 是边 AB 上一动点,连接 CD,以 AD 为直径的圆交 CD 于点 E,则线段 BE 长度的最小值为 。 7.如图5 所示,正方形 ABCD 的边长是 4,点 E 是边 AB 上一动点,连接 CE,过点 B 作 BG⊥CE 于点 G,点 P 时边 AB 上另一动点,则 PD+PG 的最小值为 。 8.如图6 所示,在矩形 ABCD 中,AB=2,AD=3,点 E、F 分别为边 AD、DC 上的点,且 EF=2,点 G 为 EF 的中点,点 P 为边 BC 上一动点,则 PA+PG 的最小值为 。 2 9.在平面直角坐标系中,A(3,0),B(a,2),C(0,m),D(n,0),且m2+n2=4,若点E 为CD的中点,则AB+BE 的最小值为 。 A.3 B.4 C.5 D.25 10.如图7 所示,AB=3,AC=2,以BC 为边向上构造等边三角形BCD,则AD 的取值范围为 。 11.如图8 所示,AB=3,AC=2,以BC 为腰(点B 为直角顶点)向上构造等腰直角三角形BCD,则AD 的取值范围为 。 12.如图9 所示,AB=4,AC=2,以BC 为底边向上构造等腰直角三角形BCD,则AD 的取值范围为 。 13.如图10 所示,AB=4,AC=2,以BC 为底边向上构造等腰直角三角形BCD,连接AD 并延长至点P,使AD=PD,则PB 的取值范围为 。 14.如图11 所示,正六边形 ABCDEF 的边长为2,两顶点A、B 分别在x 轴和 y 轴上运动,则顶点D 到 坐标原 点O的距 离 的最大 值和 最小值的乘 积 为 。3 15.如图12 所示,AB=4,点O 为AB 的中点,⊙O 的半径为1,点P 是⊙O 上一动点,△PBC是以PB 为直角边的等腰直角三角形(点P、B、C 按逆时针方向排列),则AC 的取值范围为 。 16.如图13 所示,⊙O 的半径为3,Rt△ABC ...