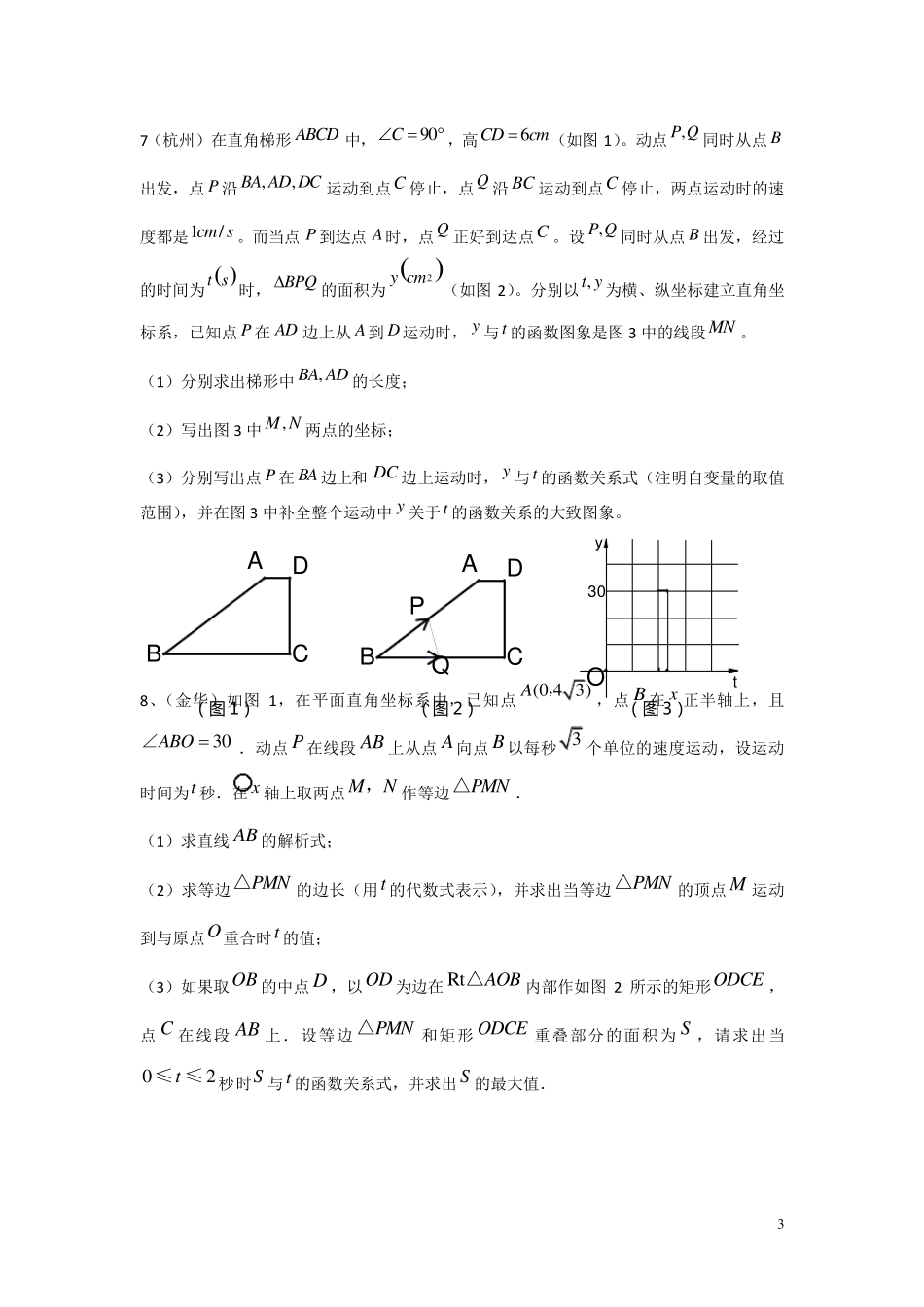
1 O M A N B C y x 初中数学动点问题练习题 1、(宁夏回族自治区)已知:等边三角形ABC 的边长为4 厘米,长为1 厘米的线段MN 在ABC△的边AB 上沿AB 方向以1 厘米/秒的速度向B 点运动(运动开始时,点M 与点A重合,点N 到达点B时运动终止),过点MN、分别作AB 边的垂线,与ABC△的其它边交于PQ、两点,线段MN 运动的时间为t秒. 1、线段MN 在运动的过程中,t为何值时,四边形MNQP恰为矩形?并求出该矩形的面积; (2)线段MN 在运动的过程中,四边形MNQP的面积为S ,运动的时间为t.求四边形MNQP的面积S 随运动时间t变化的函数关系式,并写出自变量t的取值范围. 2、如图,在梯形ABCD 中,35424 5ADBCADDCABB∥,,,,∠.动点M从 B 点出发沿线段BC 以每秒2 个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD以每秒1 个单位长度的速度向终点D 运动.设运动的时间为t秒. (1)求BC 的长. (2)当 MNAB∥时,求t的值. (3)试探究:t为何值时,MNC△为等腰三角形. 3、如图,在平面直角坐标系中,四边形OABC 是梯形,OA∥BC,点A 的坐标为(6,0),点B的坐标为(4,3),点C 在y 轴的正半轴上.动点M 在OA 上运动,从 O 点出发到A 点;动点N 在AB 上运动,从 A 点出发到B 点.两个动点同时出发,速度都是每秒1 个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒). (1)求线段AB 的长;当 t 为何值时,MN∥OC? (2)设△CMN 的面积为S,求S 与t 之间的函数解析式, 并指出自变量t 的取值范围;S 是否有最小值? 若有最小值,最小值是多少? C P Q B A M N A D C B M N 2 EDBCAQP(3)连接AC,那么是否存在这样的t,使MN 与AC 互相垂直? 若存在,求出这时的t 值;若不存在,请说明理由. 4、(河北卷)如图,在Rt△ABC 中,∠C=90°,AC=12,BC=16,动点 P 从点 A 出发沿AC 边向点 C 以每秒 3 个单位长的速度运动,动点 Q 从点 C 出发沿 CB 边向点 B 以每秒 4 个单位长的速度运动.P,Q 分别从点 A,C 同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,△PCQ 关于直线 PQ 对称的图形是△PDQ.设运动时间为 t(秒). (1)设四边形 PCQD 的面积为 y,求y 与t 的函数关系式; (2)t 为何值时,四边形 PQBA 是梯形? (3)是否存在...