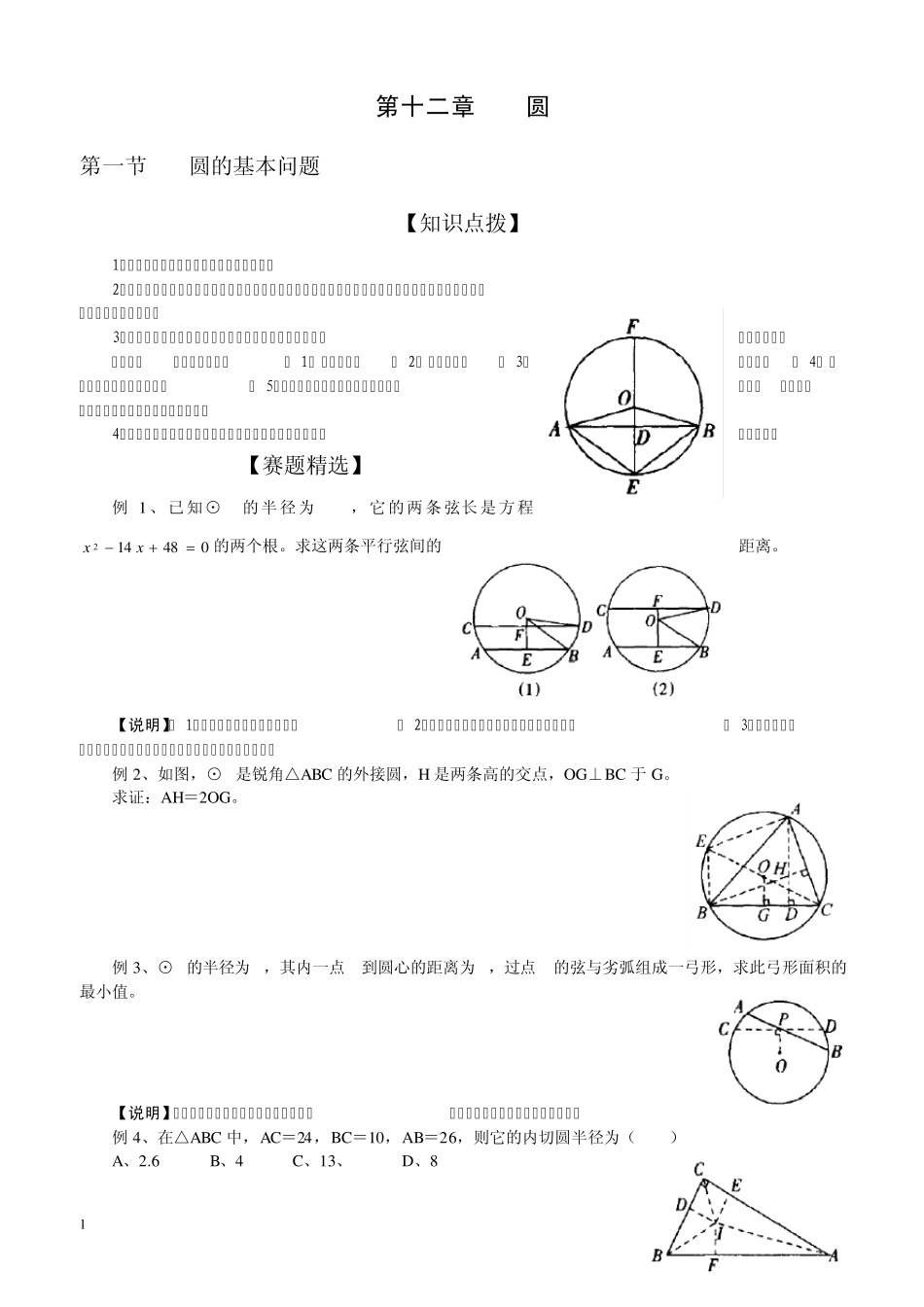
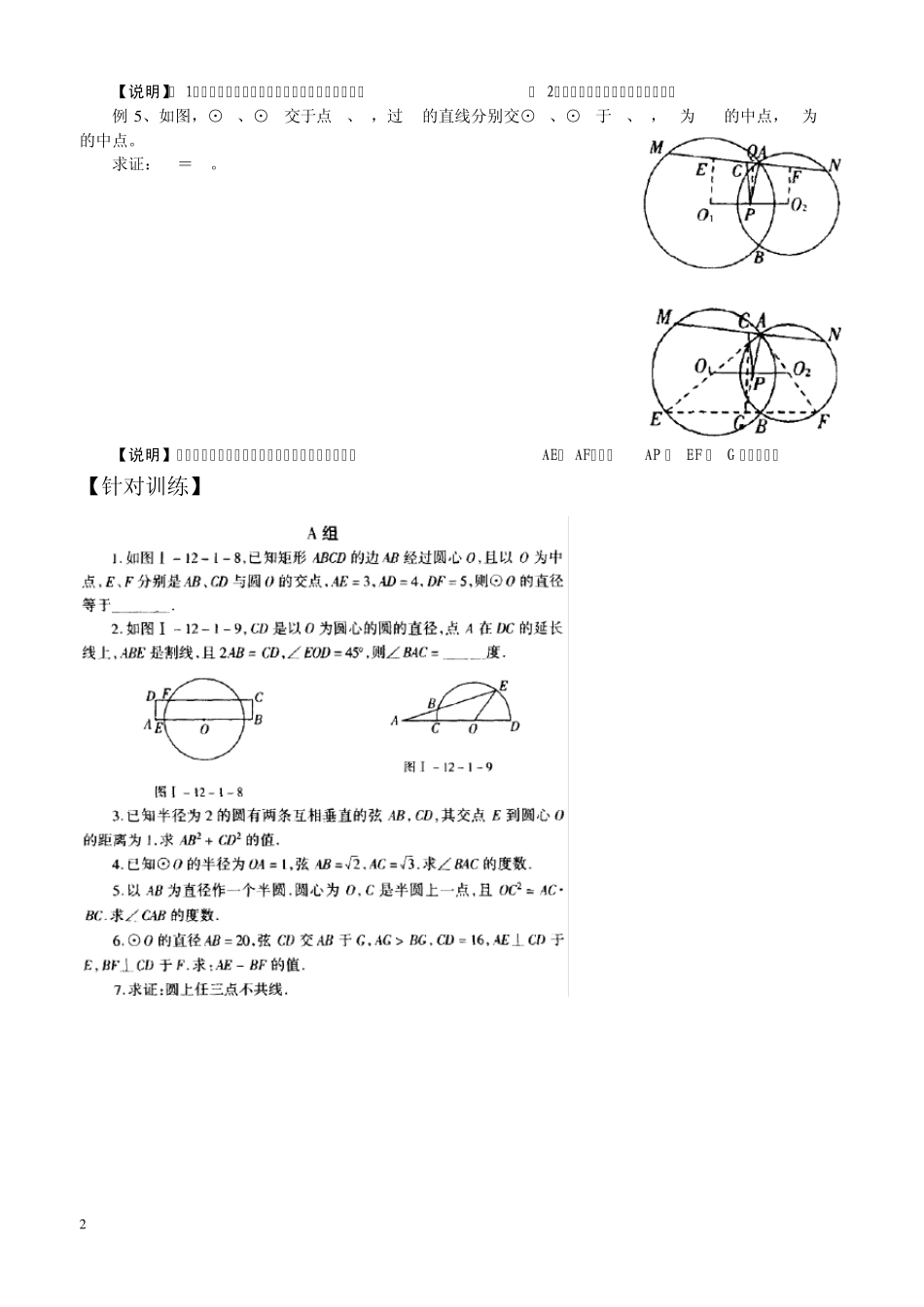
1 第十二章 圆 第一节 圆的基本问题 【知识点拨】 1、不在同一直线上的三点可以确定一个圆。 2、圆既是轴对称图形,又是中心对称图形,它具有旋转对称性。这是圆最基本最重要的性质,是证明垂径定理的有力工具。 3、垂径定理:垂直于弦的直径平分这条弦,并且平分这弦对的两条弧。 实际上,一直线只要满足( 1) 经过圆心、( 2) 垂直于弦、( 3)平分弦、( 4) 平分弦所对的弧中的一条、( 5)平分弦所对弧中的另一条;在这五条中,只要有两条是正确的,则其他三条必然成立。 4、如图,它是关于垂径定理及其推论的基本图形,一定要很好掌握。 【赛题精选】 例1、已知⊙O的半径为 5cm,它的两条弦长是方程048142xx的两个根。求这两条平行弦间的距离。 【说明】( 1)要注意定理的条件及选择;( 2)关于垂径定理及推论的基本图形要记清;( 3)要能考虑到图中的两条平行弦相对于圆心有两种可能的位置关系。 例2、如图,⊙O是锐角△ABC 的外接圆,H 是两条高的交点,OG⊥BC 于 G。 求证:AH=2OG。 例3、⊙O的半径为 2,其内一点P到圆心的距离为 1,过点P的弦与劣弧组成一弓形,求此弓形面积的最小值。 【说明】圆的旋转对称性是圆的最基本的性质,要善于抓住这一性质处理相关问题。 例4、在△ABC 中,AC=24,BC=10,AB=26,则它的内切圆半径为( ) A、2.6 B、4 C、13、 D、8 2 【说明】( 1)此法对求任何三角形的内切圆的半径均适用;( 2)另本题还可用切线长定理求解。 例5 、如图,⊙O1、⊙O2交于点 A、B,过 A的直线分别交⊙O2、⊙O3于 M、N,C为 MN的中点,P为 O1O2的中点。 求证:PA=PC。 【说明】本例主要用垂径定理证明,如按下图作两圆的直径AE、 AF,延长AP 交 EF 于 G 也可证明。 【针对训练】 3 4 第二节 和圆有关的角 【知识点拨】 和圆有关的角有五种:圆心角、圆周角、圆内角、圆外角、弦切角。圆周角是五种角的核心。本节只探讨前四种与圆有关的角,其中后两种角的概念及这四种角的有关性质如下: 1、 顶点在圆内的角叫圆内角(圆心角是圆内角的特殊情形); 2、 顶点在圆外,两边与圆相交的角叫圆外角; 3、 度数定理 ( 1) 圆心角的度数等于它所对的弧的度数。 (2) 圆周角的度数等于它所对弧的度数的一半。 (3) 圆内角的度数等于它和它的对顶角所对的两条弧度数和的一半。 (4) 圆外角的度数等于它所夹的两弧度数的差...