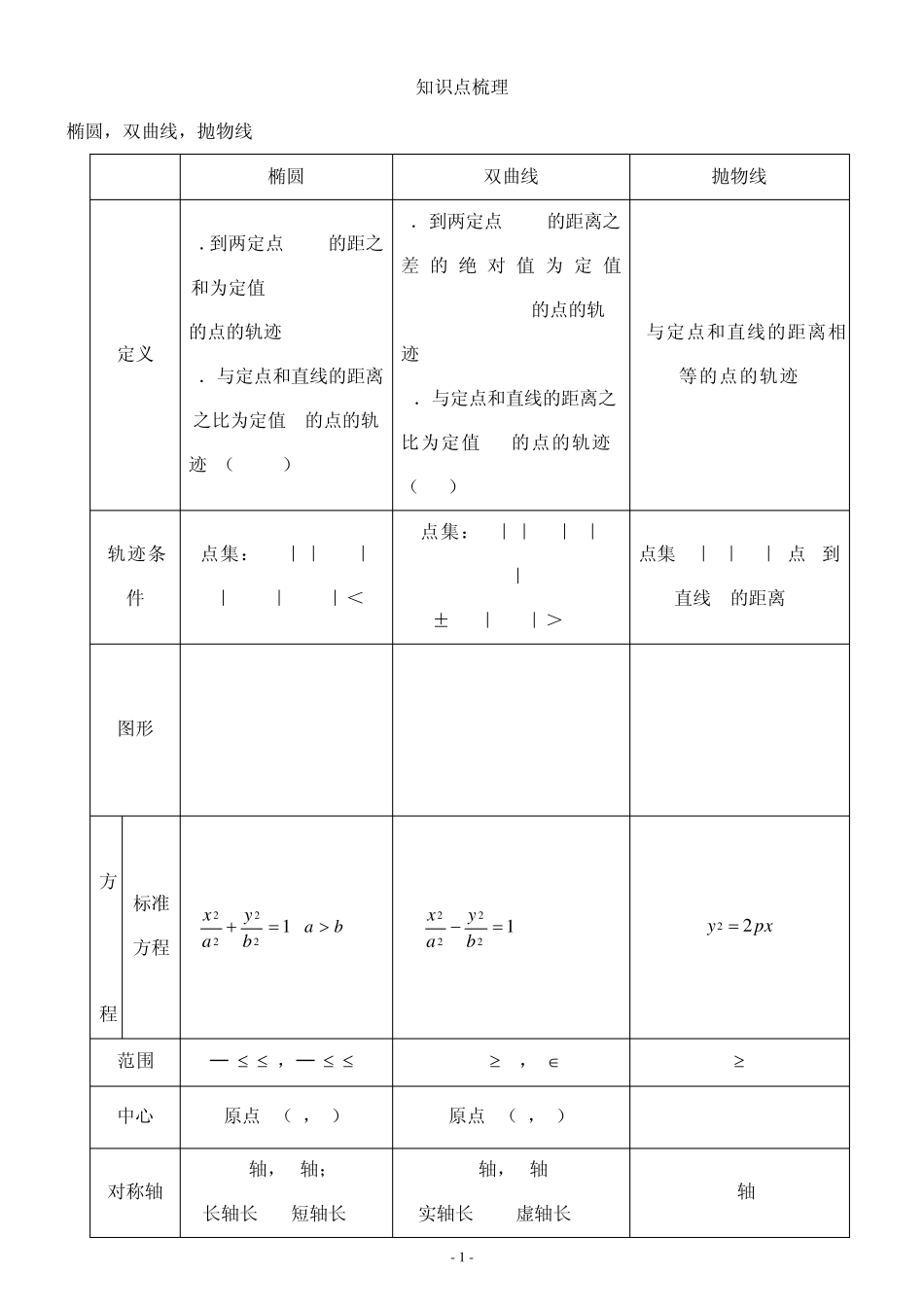
- 1 - 知识点梳理 椭圆,双曲线,抛物线 椭圆 双曲线 抛物线 定义 1.到两定点F1,F2的距之和为定值2a(2a>|F1F2|) 的点的轨迹 2.与定点和直线的距离之比为定值e的点的轨 迹.(01) 与定点和直线的距离相等的点的轨迹. 轨迹条件 点集:({M||MF1+|MF2|=2a,|F 1F2|<2a 点集:{M||MF1|-|MF2|. =±2a,|F2F2|>2a}. 点集{M| |MF|=点M到直线l的距离}. 图形 方 程 标准方程 12222byax(ba >0) 12222byax(a>0,b>0) pxy22 范围 ─axa,─byb |x| a,y R x0 中心 原点O(0,0) 原点O(0,0) 对称轴 x轴,y轴; 长轴长 2a,短轴长 2b x轴,y轴; 实轴长 2a, 虚轴长 2b. x轴 - 2 - 焦点 F1(c,0), F2(─c,0) F1(c,0), F2(─c,0) )0,2( pF 准 线 x=± ca 2 准线垂直于长轴,且在椭圆外. x=± ca 2 准线垂直于实轴,且在两顶点的内侧. x=-2p 准线与焦点位于顶点两侧,且到顶点的距离相等. 焦距 2c (c=22ba ) 2c (c=22ba ) 离心率 )10(eace )1( eace e=1 【备注 1】双曲线: ⑶等轴双曲线:双曲线222ayx称为等轴双曲线,其渐近线方程为xy,离心率2e. ⑸共渐近线的双曲线系方程:)0(2222byax的渐近线方程为02222byax如果双曲线的渐近线为0 byax时,它的双曲线方程可设为)0(2222byax. 【备注 2】抛物线: (1)抛物线2y =2px(p>0)的焦点坐标是(2p ,0),准线方程 x=-2p ,开口向右;抛物线2y =-2px(p>0)的焦点坐标是(-2p ,0),准线方程 x=2p ,开口向左;抛物线2x =2py(p>0)的焦点坐标是(0,2p ),准线方程 y=-2p ,开口向上; 抛物线2x =-2py(p>0)的焦点坐标是( 0,-2p ),准线方程 y=2p ,开口向下 . (2)抛物线2y =2px(p>0)上的点M(x0,y0)与焦点F的距离20pxMF;抛物线2y =-2px(p>0)上的点M(x0,y0)与焦点F的距离02xpMF (3)设抛物线的标准方程为2y =2px(p>0),则抛物线的焦点到其顶点的距离为2p ,顶点到准线的 - 3 - 距离2p ,焦点到准线的距离为p. (4)已知过抛物线2y =2px(p>0)焦点的直线交抛物线于A、B两点,则线段AB称为焦点弦,设A(x1,y1),B(x2,y2),则弦长AB =21xx...