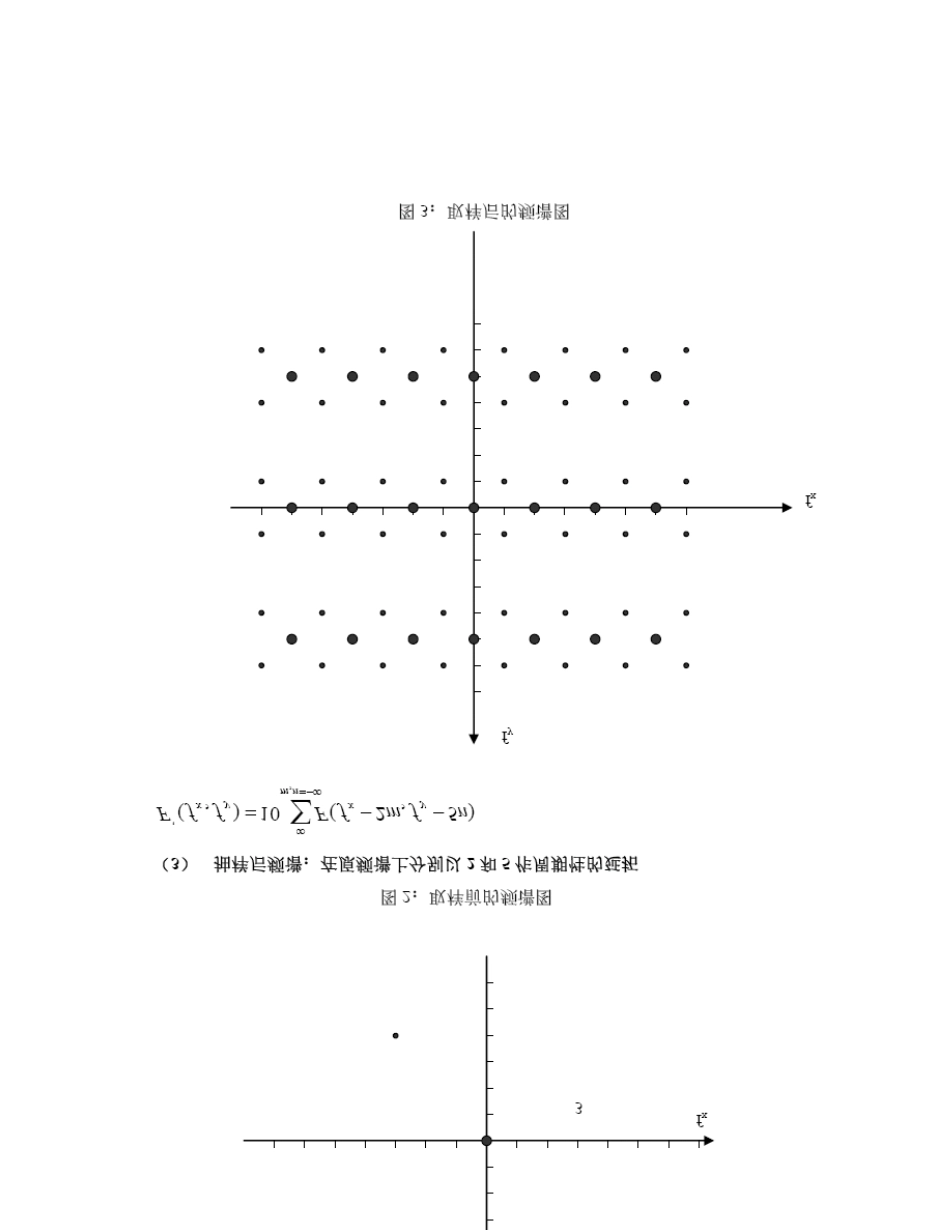
2-3(1)由图(a)和图(b)可知,在长为 0.1 米的屏幕上光栅变化 2.5 次,在高为0.1 米的屏幕上光栅变化 3 次,所以f =25(周/米)xf =30(周/米)y(2)光栅的周期与空间频率的表达式:T= 1/f ;T= 1/fxxyy光栅的方位角与空间频率的表达式:f =;f =xdxd(x)Ψydyd(y)Ψ(3)负的时间时间频率没有物理意义,负的时间频率是在对 cos 函数用欧拉公式的时候引入的,只是数学形式上的表达。负的空间频率与负的时间频率一样没有物理意义。2-42-6由书上的公式 2-17f=maxfffZkKkHWfnkkKHW221221.2..2.=根据第 5 题的数据 =0.92,=0.81,=W/H=16/9,K=0.71k2kα当隔行扫描时,=25,Z=1152fff=23.5MHzmax25*1152*81.0*292.0*7.0*9162≈当逐行扫描时,=50,ff所以f=2f47M'maxmax ≈2-11由图中可以看出,对每帧图像,两种格式的数据量相同; 对于色度信号的分辨率,水平方向上,4:1:1格式是4:2:0格式的一半;垂直方向上 4:2:0格式是4:1:1格式的一半; 对于亮度信号分辨率,4:1:1格式与4:2:0格式在水平和垂直方向上是一致的。 3 -3 3 -1 7 题目修改如下: 对MV 序列{-2,-1,0,2}进行编码; 用一般算术编码,取9 比特精度(允许最后一位不能正确解码)。 解: MV 概率如下: -2:1/16 -1:1/4 0:3/8 1:1/4 2:1/16 待编码的MV 序列为:{-2,-1,0,2} 符号 -2 -1 0 1 2 概率(十进制) 1/16 1/4 3/8 1/4 1/16 概率(二进制) .0001 .01 .011 .01 .0001 累积概率 0 .0001 .0101 .1011 .1111 第一个符号-2: C=0+1×0=0 A=1×0.0001=0.0001 第二个符号-1: C=0+0.0001×0.0001=0.00000001 A=0.0001×0.01=0.000001 第三个符号0: C=0.00000001+0.000001×0.0101=0.0000001001 A=0.000001×0.011=0.000000011 第四个符号2: C=0.0000001001+0.000000011×0.1111=0.0000001110101 A=0.000000011×0.0001=0.0000000000011 所以,MV 序列{-2,-1,0,2}经过算术编码后的序列为 : 0.0000001110101 1. 附加题参考答案: 从优化的观点看,编码的优化目标是最小化平均码长。如果对出现频率低的符号也制定变长编码表,出现频率高的符号的码长会增加,而对出现频率低的符号单独编码,虽然频率低的符号码长会增加,但由于它们的出现频率低,整体的平均码长反而会降低。总之,会有一个最优点,但这个点肯定不会是对全部符号制定变长编码表,必须对一部分出现频率相对低的符号单独编码。 4-4 图...