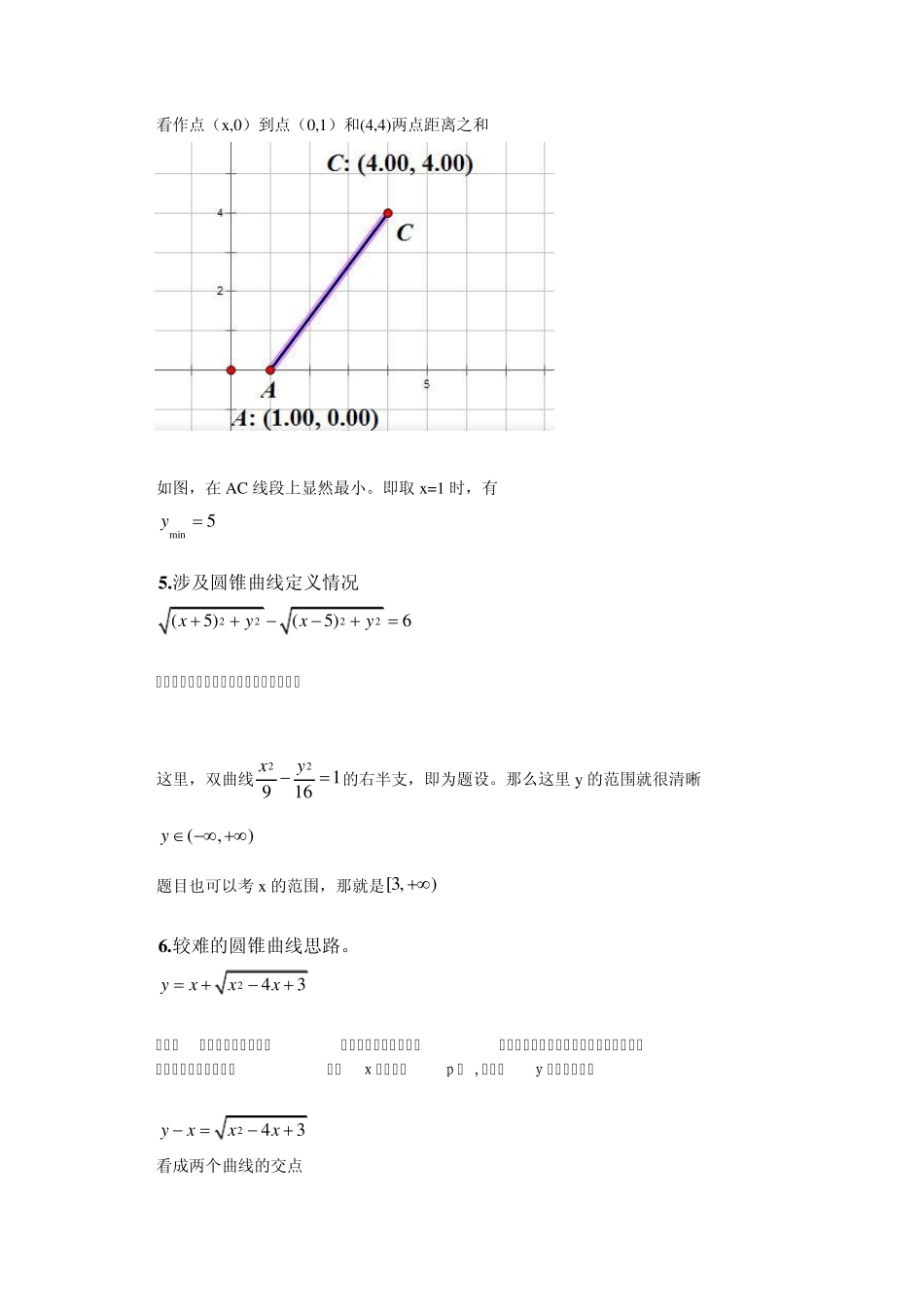
带根号的函数最值问题 数学中,求函数最值本身是一块很难很重要的内容。当函数解析式中出现根号的时候,难度会加大。这里,就高中范围内出现的带根号的函数最值问题小小地总结一下。 1 . 单调性一致情况 21yxx (x ∈[1,2]) 分析:这个函数,分成两部分。 x 是增的,21x 也是增的。这个函数21yxx在定义域上单调增 于是,最大值最小值就在端点时取到。 minmaxy13,25y 2 .单调性不一致的根号中一次项情况 yx1x (x ∈[0,1]) 分析:单调性不一致,首先考虑换元法 令21=t(t[0,1]),x =1-tx maxmin3 ,14yy 3 .根号中出现二次项情况 21yxx (x ∈[-1,1]) 分析:单调性很难判断。这时候首先考虑换元法 方法一:三角换元 我们知道,三角函数cos 、sin 的范围本身就是[-1,1],代入以后可以一可以用三角公式进行运算,开阔思路,二则去掉根号,简化运算。 设 x =cos ,这里为了确定范围,不失一般性,设[0,], 利用 1-2cos =sin 2 ,去掉根号很方便。 21cossin2 sin()4yxx 值域就是[ 1,2] 方法二:移项平方 这是我们自初中以来所谓的去根号的最“喜欢”的方法。但有时候,它是那么的吃力不讨好。 2211yxxyxx 两边平方 222y21xyxx 注意到这里平方的条件是y≥x 222x210yxy 由于 x 存在,判别式大于等于 0 22248(1)840[2,2]yyyy 但要注意到,y≥x ,于是有 y≥-1 [ 1,2]y 方法三:求导 求导属于暴力流,但是往往是在你绝望的时候唯一能抓的稻草。本文大部分题目可以用求导解决。 221'11yxxxyx 令 y’≥0 解得2[ 1,]2x ,不过这个过程颇为艰辛 于是易得[ 1,2]y 4 .双根号明显数形结合的情况 221(4)16yxx 求最小值 分析:明显可以看作两点间距离公式类型。这类题难度不大。但要注意,当括号内平方是展开状况的时候,要学会主动去配方发现。 看作点(x,0)到点(0,1)和(4,4)两点距离之和 如图,在AC 线段上显然最小。即取 x=1 时,有 min5y 5 .涉及圆锥曲线定义情况 2222(5)(5)6xyxy 分析:这类题就是很典型的圆锥曲线定义 这里,双曲线221916xy 的右半支,即为题设。那么这里 y的范围就很清晰 (,)y 题目也可以考 x的...